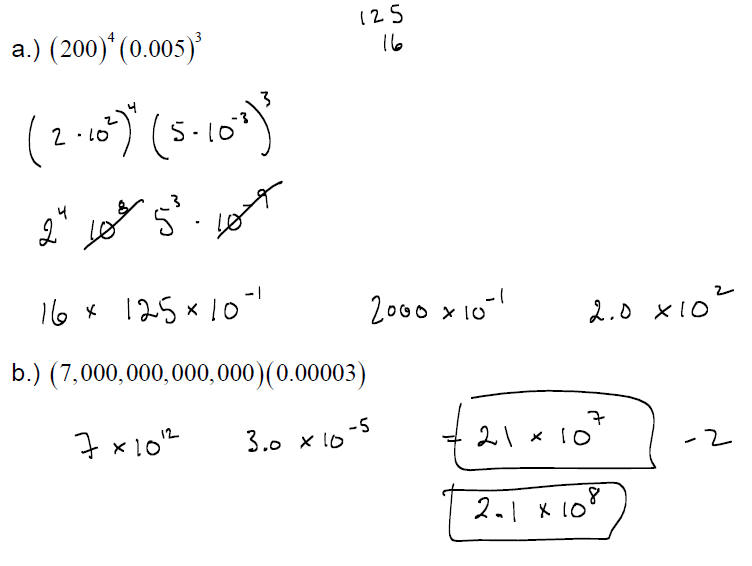NEGATIVE INTEGERS
Consider the quotient:
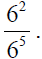
Apply the quotient rule :
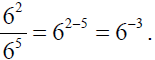
Now divide out common factors of 6:
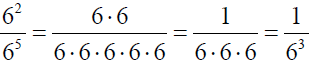
We see that
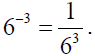This suggests the following definition of negative
exponents.
If x is any nonzero real number and n is a natural number, then
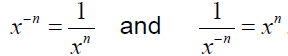
EXAMPLE: Evaluate
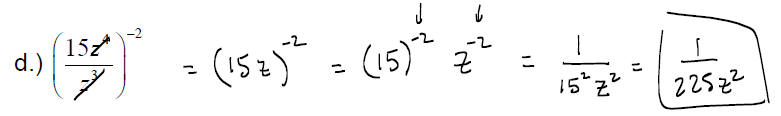
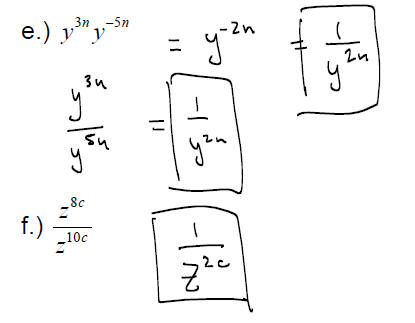
Use the properties of exponents to write the result without using negative
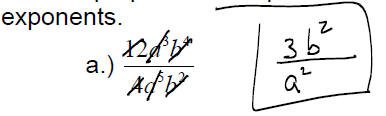
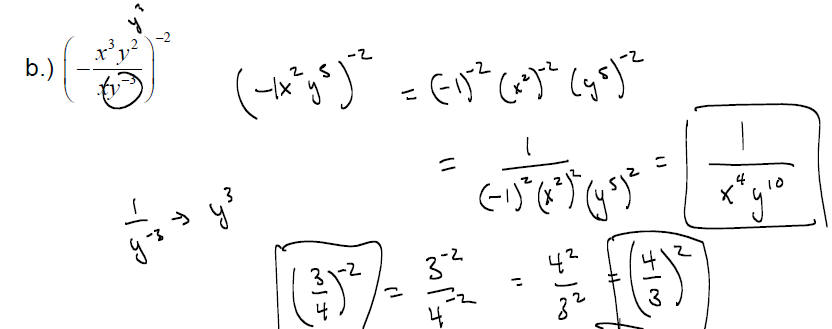
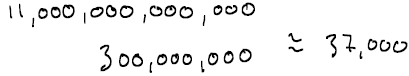
SCIENTIFIC NOTATION:
Many numbers that appear in science are either extremely large or very
small. This makes it hard to write and say these numbers quickly. An
effective way of writing these numbers is called scientific notation.
The distance from the sun to earth is about 93,000,000 miles
The probability of being dealt a royal flush in poker is 0.00000154
A number written in scientific notation has the form:
A×10n where 1≤ A <10 and n is any integer.
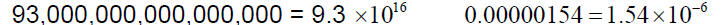
EXAMPLE: Determine if the numbers are in scientific
notation:
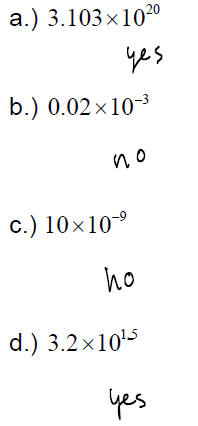
Large numbers have positive powers on 10 and small numbers
have negative
powers on 10.
When multiplying by a power of 10, move the decimal the
same number of
places as the exponent . If the exponent is positive , move to the right; if the
exponent is negative , move to the left.
EXAMPLE: Write in decimal notation
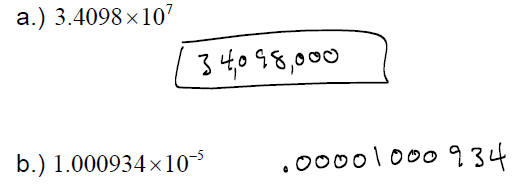
To Write a Number from Decimal Notation into Scientific
Notation:
• Move the decimal to the right of the first nonzero digit . This will
make the first number greater than or equal to 1 but less than 10.
• Suppose we moved the decimal n places. If you moved to the
left, use a positive n as the exponent ; if you moved to the right,
use a negative n as the exponent .
EXAMPLE: Write the numbers in scientific notation:
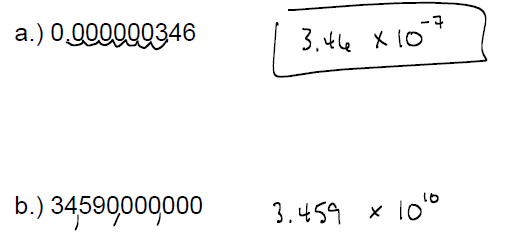
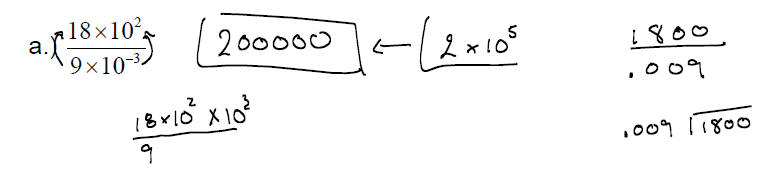
EXAMPLE: Perform the indicated computations, writing the
answer in decimal
notation without the use of exponents.
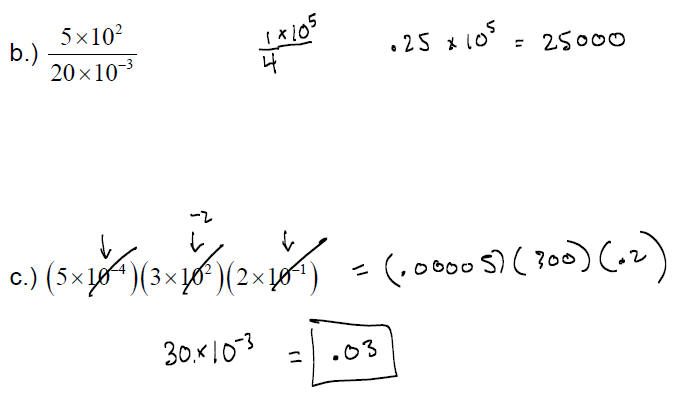
EXAMPLE: Perform the indicated computations, writing the
answer in
scientific notation
