2 A negative result and further observations
Lemma 2.1 Let m, n and v be positive integers such that m ≠ n. A ring
containing elements a and b such that
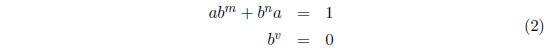
is trivial.
Proof: Assume a and b are elements satisfying (2) . Since
m ≠ n we
may by left-right symmetry assume m > n to hold. Define the weight of a
monomial in a and b by
w (a) = -(2n + 1), w(b) = 2
letting the weight of a product be the sum of the weights of its factors.
Consider all monomials of the form
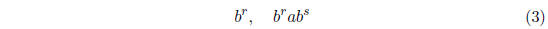
with r ≥ n and s ≥ 0. We claim that these are
all 0. Clearly this is true
for such a monomial having weight ≥ 2v, since it must have a factor b v. We
can work by downward induction, assuming that all monomials of the form
(3) of higher weight than the monomials we are looking at equal 0.
Consider first a monomial of the form br. We have
.
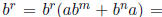
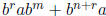The summand
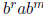has weight higher than br, while the
summand
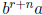is left divisible by
,
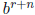and this factor certainly has weight
greater than that of br. So our monomial is zero as desired.
It remains to consider a monomial of the form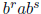 
. Since r
≥ n, this has an
internal factor b na, which can be replaced by 1-abm, which by our choice of
weights consists of summands of weight > w(bna), hence we have expressed
our monomial as a linear combination of monomials of greater weight, and
clearly each of the form (3). So again, our monomial is zero .
So all monomials of the form (3) are 0, in particular, bn = 0, substituting in
to the equation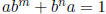 
we get 1 = 0.
Corollary 2.2 For a positive rational number q ≠ 1 we have
.
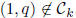For our last observation we begin with
Lemma 2.3 For all k and all positive integers m and n
there are (m+n) ×
(m + n) matrices a and b over k satisfying
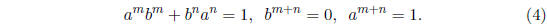
Proof: Write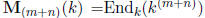 
and let
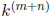have
the usual
basis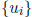 
. Define a and b as follows
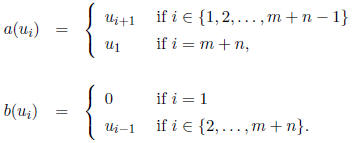
Clearly a and b satisfy (4).
Theorem 2.4 For all positive rational numbers q and all nonnegative integers
M and N we have
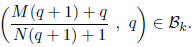
Proof: Since q is a positive rational number one can write
q = m/n for
some positive integers m and n. We get
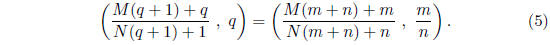
Because of the equation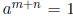 
in Lemma 2.3, the
elements a and b of
that lemma satisfy (1) where i = M(m + n) + m and j = N(m + n) + n,
and hence the right hand side of (5) lies in
.
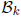Given positive integers i and j we notice that
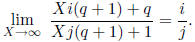
So with this in mind we get the following summary:
Corollary 2.5 For a field k and positive rational numbers p
and q we have
the following:
1. 
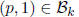for all p.
2. 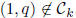for all q ≠ 1.
3. 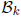and
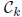are dense subsets in the usual topology of the
first quadrant
of the real plane . 2
Acknowledgement: I would like to thank my advisor George M. Bergman
for many good suggestions and simplifications when I was writing this paper.
References
[1] G. Agnarsson, S.A. Amitsur, J.C. Robson, Recognition of Matrix Rings
II, Israel Journal of Mathematics (to appear), accepted in April 1995.
