One-to-one, Onto, and Inverse Functions

• In this section, we will look at three special
classes of functions and see how their properties
lead us to the theory of counting.

• So far, we have the general notion of a function
f: X → Y, but in terms of the comparative sizes
of the three sets involved (X, Y and f ), all we
can say is that |f | = |X|.

• In this section, we compare |X| with |Y|.

One-to-one Functions

• Definition: A one-to-one (injective) function f
from set X to set Y is a function such that each
x in X is related to a different y in Y .

• More formally, we can restate this definition as

either:
 f :X → Y is 1-1 provided
f(x₁) = f(x₁) implies x₁ = x₂,

or f :
X → Y is 1-1 provided
x₁ ≠ x₂ implies f(x₁) ≠ f(x₂).

Illustrative Examples

• The function below is 1-1:

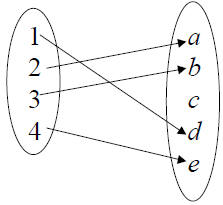
This function is not:

Proving Functions Are 1-1

• If f: R→ R is given by f (x) = 3x + 7, prove it is
one-to-one.

• Proof: Assume f (a) = f (b). Show a = b.

Now f (a) = f (b) means 3a + 7 = 3b + 7, so
3a = 3b, therefore a = b.

• Why is f: R → R given by f (x) = x² not 1-1?

• Since 9 = f(3) = f(-3), but 3 ≠ -3, the definition is
violated.

Onto Functions

• Definition: A function f: X → Y is said to be onto
(surjective) if for every y in Y, there is an x in X
such that f (x) = y.

• This can be restated as: A function is onto when
its image equals its range, i.e. f (X) = Y.

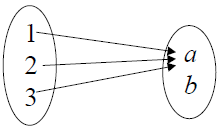
• Examples:

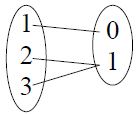
ONTO

NOT ONTO

Testing Onto For Infinite Functions

• Show that f: R → R given by f (x) = 5x - 7 is onto.

• Let y be in R. Then (y + 7) and (y + 7)/5 are also
real numbers .

Now f( (y + 7)/5 ) = 5[(y + 7)/5] - 7 = y, hence
if y is in R, there exists an x in R such that
f (x) = y.

• Is f: R→ R given by f (x) = 1/x onto?

• No! There is no x in R that has output = 0.

One-to-one Correspondences

• Definition: A function is called a one-to-one
correspondence (bijection) if it is one-to-one and
onto.

• One-to-one correspondences define the theory of
counting. Why?

• If f: X → Y is one-to-one, then |X| ≤ |Y|, and if f
is onto, then |X|≥ |Y|, so if f is both, |X| = |Y|.

• Hence, to count the elements of an unknown set ,
we create a 1-1 correspondence between the set
and a set of known size. Simple !

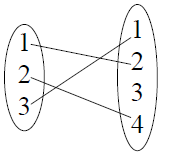
Inverse Functions

• Recall that the inverse relation is created by
inverting all the ordered pairs that comprise the
original relation.

• When is the inverse of a function itself a
function?

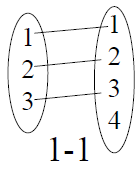
not onto (f -1 not def.)

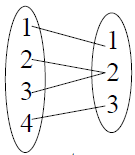
onto not 1-1 (f -1 not well-def.)

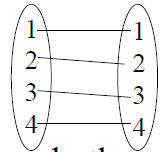
both (f -1 is a function)

Finding Inverse Functions

• Theorem: If f: X → Y is a one-to-one and onto,
then f ^-1 is a one-to-one and onto function.

• Given f , how do we find f ^-1?

• Let f: R → R be given by f (x) = 4x - 1 = y. Now,
swap x and y and solve for y :

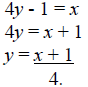
• Thus f ^-1 (x) = (x + 1)/4.