Problem 1.33
For each value of the exponent e , we have 2t possible floating point numbers,
where t is the number of bits used
by the mantissa f in a floating point number (1 + f) × 2e. For example, if t = 3,
for a given exponent e, we can
represent the 8 numbers: 000 001 010 011 100 101 110 111
With a given emax and emin, there are emax − emin + 1 intervals. So overall,
we have
(emax − emin + 1) × 2t
floating point numbers.
In the file floatgui.m, we would have:
% Exercise:
% How many "floating point" numbers are in the set ?
% Complete this statement.
numfloats = (emax - emin + 1)*2^t;
text(.9*xmax,2,num2str(numfloats))
Or, you may notice that floatgui.m stores all of the calculated floating
point numbers in a vector F. So you
could also just use
% Exercise:
% How many "floating point" numbers are in the set?
% Complete this statement.
text(.9*xmax,2,num2str(length(F)))
Problem 1.34
In exact arithmetic, for any number n
n/10 − n*(0.1) = 0
However, in MATLAB we see:
>> t = 0.1;
>> n = 1:10;
>> e = n/10 - n*t
e =
1.0e-15 *
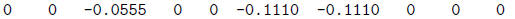
This occurs because we cannot represent the base-ten number 0.1 exactly in
binary arithmetic with a finite
number of bits. In double precision floating point arithmetic, this number is
rounded to 52 bits, so represented
inexactly. This is also true of many other numbers that we can represent exactly
in base ten.
In the sequence above, the computed numbers with n = 3, 6, and 7 have n/10
rounded differently than n *t,
since t was already approximate. So these three numbers are not zero on the
computer . (You can see this by
looking at n/10 and n*t using format hex).
Problem 1.38
Given a quadratic equation
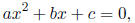
its roots (in exact arithmetic) are given by the classic quadratic formula
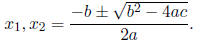
For the given coefficients a = 1, b = −100000000, c = 1, MATLAB’s roots
function gives (using format long
e to see more precision):
>> a = 1;
>> b = -100000000;
>> c = 1;
>> roots([a b c])
ans =
9.999999999999999e+07
1.000000000000000e-08
or approximately 108 and 10-8. Computing “by hand” using the quadratic formula
gives:
>> x1 = (-b + sqrt(b*b - 4*a*c))/(2*a)
x1 =
100000000
>> x2 = (-b - sqrt(b*b - 4*a*c))/(2*a)
x2 =
7.450580596923828e-09
In MATLAB, the quadratic formula computed
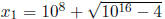reasonably accurately, but was much worse
on
,
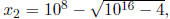where we are subtracting two large numbers of very similar value. Instead, we
can use
the quadratic formula to compute x1, then compute x2 using the formula x1x2 =
c/a, i.e.,
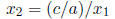
giving more accurate roots for this quadratic:.
>> x1 = (-b + sqrt(b*b - 4*a*c))/(2*a)
x1 =
100000000
>> x2 = (c/a)/x1
x2 =
1.000000000000000e-08
Problem 1.40
a. There are 16 pictures hidden in the data.
b. The picture is just a big matrix of pixel values, where each pixel has a
floating point number that defines
its color (or grayscale value). So if the picture you see with image has n2
pixels, it is just an n × n matrix,
where each entry in the matrix represents the color at that pixel. Each of these
matrix elements is a floating
point number, which means that it gets 52 bits worth of information in its
mantissa. In steganography, other
images are hidden in the original picture by using the lower order bits . For
example, the picture of the boy
is defined by the first 5 binary digits in the mantissa . The next 5 bits of each
pixel define grayscale values
for the next picture (the first dog picture), the next 5 bits are another dog
picture, etc. We don’t have to
use the same number of bits for each picture. A simple black and white picture
can be represented by just
one bit per pixel. There are, for example, three separate black and white
pictures using one bit each in bits
16, 17, 18, and 19.
Because you are adding each picture to the end of the
mantissa, when we look at the full floating point
number (with image) the main picture (of the boy) dominates. The stegano program
lets us look at the
different bits of the mantissa separately and see the individual pictures.
