Monitoring Student Progress
• The process of collecting and evaluating data to
make decisions about the adequacy of student
progress toward a goal and/or responding to
instruction or interventions
• Evaluation of student rate of change (slope) as
compared to the slope of anticipated progress
• Requires:
– Technically sound measures
– Multiple forms of the same measure
– Assessment systems that are sensitive to student growth
– Standardized administration procedures
– Frequent measurement (occurs at least monthly)
Research Supports the Use of
Progress Monitoring
• Progress monitoring data produce accurate,
meaningful information about students’ academic
levels and their rates of improvement
• Progress monitoring data are sensitive to student
improvement
• Performance on progress monitoring measures
corresponds well to performance on high-stakes tests
• When teachers use progress monitoring data to
inform their instructional decisions, students make
greater learning gains
Process of Progress
Monitoring
• Progress monitoring is a data-based
instructional decision making tool
• Steps for using data :
– Gather baseline performance data
– Set instructional goals
– Provide targeted instruction
– Monitor progress toward goal
– Adjust goal upward or modify instruction as
needed
Example of Progress
Monitoring Data
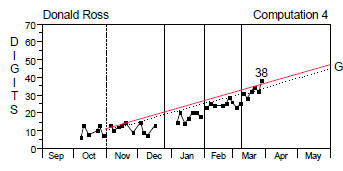
Features of Progress
Monitoring Systems
• Data are collected and evaluated frequently
– Schedule is determined by goal and current level of student
performance
– Typically ranges from 2 times per week to monthly
• Teachers may choose to monitor progress of
all students in class
• Typically, students at-risk of failure are
assessed until they reach proficiency
• Data-based decision rules are applied to
graphed data to determine when goals should
be raised or instruction should be modified
Measuring Secondary
Students’ Progress in
Mathematics
• Development of progress monitoring
measures for secondary grades (especially
beyond general math) is in its infancy
• Project AAIMS is developing and validating
measures for pre -algebra and first year
algebra
• Algebra measures have been created using
both the robust-indicators and the curriculum-sampling
methods
Algebra Progress Monitoring
Research Results
• Project AAIMS evaluates technical adequacy and
teachers’ use of algebra measures
• Reliability, criterion validity, and sensitivity to growth
over time is documented for the Basic Skills, Algebra
Foundations, and Content Analysis-Multiple Choice
measures
• Less data on the Translations measure due to
mismatch with existing curriculum materials in
participating school districts
• Research is on-going to continue refinement of the
measures
Examples of Algebra Progress
Monitoring Measures
• Basic Skills
• Algebra Foundations
• Translations
• Content-Analysis-Multiple Choice
Basic Skills in Algebra
• Robust indicator of pre-algebra/algebra proficiency
• Problems include:
– Solving basic “fact” equations
– Applying the distributive property
– Working with integers
– Combining like terms
– Simplifying expressions
– Applying proportional reasoning
• Timed administration
• Constructed-response items
• Scored by counting number of problems correct
Basic Skills
Solve:
9 + a = 15
a = |
Solve:
10 – 6 = g
g = |
Evaluate :
12 + ( – 8) + 3 |
Simplify :
9 – 4 d + 2 + 7 d |
Simplify :
2 x + 4 + 3 x + 5 |
Simplify :
5( b – 3) – b |
Solve:
12 – e = 4
e = |
Solve:
q • 5 = 30
q = |
Simplify :
4(3 + s ) – 7 |
Evaluate :
8 – ( – 6) – 4 |
Simplify :
b + b + 2 b |
Simplify :
2 + w (w – 5) |
Sol v e:
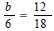 b b
b = |
Solve:
1 foot =12 inches
5 fee t = _ _ _ _ inches |
Simplify :
7 – 3( f – 2 ) |
Simplify :
4 – 7 b + 5 ( b – 1) |
Evaluate :
– 5 + ( – 4) – 1 |
Simplify :
s + 2 s – 4 s |
Solve:
63 ÷ c = 9
c = |
Solve:
x + 4 = 7
x = |
Simplify :
2( s – 1) + 4 + 5 s |
Simplify :
– 5( q + 3) + 9 |
Simplify :
8 m – 9( m + 2) |
Evaluate :
9 + ( – 3) – 8 |
Algebra Foundations
• Robust indicator of pre-algebra/algebra proficiency
• Problems include:
– Writing and evaluating variables and expressions
– Computing expression (integers, exponents, and order of
operations )
– Graphing expressions and linear equations
– Solving 1-step equations and simplifying expressions
– Identifying and extending patterns in data tables
• Timed administration
• Constructed-response items
• Scored by counting number of problems correct
Algebra Foundations
Content Analysis
• Curriculum sampling approach to algebra
proficiency
• Problems are sampled from core concepts in
the first 2/3 of a traditional Algebra 1 textbook
• Multiple-choice items with partial credit
• Scored by counting number of points earned
– Up to 3 points per problem awarded using a
scoring rubric
– -1 point penalty for circling an incorrect answer
without showing any work (guessing)
Content Analysis - Multiple Choice
Evaluate b2 - a2
when a = 4 and
b = 5a) 21
b) 1
c) 11
d) 9 |
Rewrite this
expression without
parentheses:
(-5) (4 – y)a) 9 - y
b) -20 + 5y
c) -1 – 5y
d) -20 – 5y |
Solve:
2t – 5 = 7
a) 1/2
b)6
c) 1
d)2 |
Solve:
y/3 = 4
a) -10
b)7
c) 4/3
d)12 |
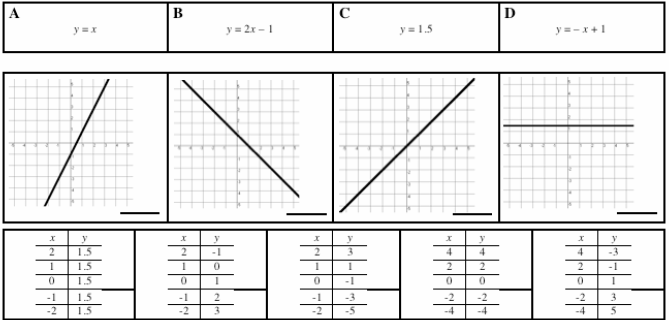
Which line on the
graph is
y = 2?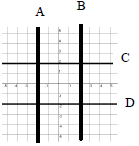
a) Line A
b) Line B
c) Line C
d) Line D |
Which line on the
graph is
y + 2x = 4 ?
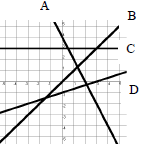
a) Line A
b) Line B
c) Line C
d) Line D |
Write the equation
in slope-intercept
form:
m = ( 1/2 ) b = 3
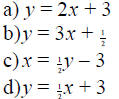
|
Rewrite this
equation in
standard form
using integer
coefficients.
-4y + 1/2x = 2
a) -8y + 2x = 4
b)x – 8y = 4
c) y = 4x + 8
d)4y – 2x = 4 |
Translations
• Robust indicator of pre-algebra/algebra proficiency
• Problems include:
– Tasks drawn from Connected Mathematics Project (CMP)
Curriculum
– Translate representations for relationships between two
variables
• Data tables
• Graphs
• Equations
• Story scenarios
• Timed administration
• Scored by counting number of problems correct and
subtracting number of problems incorrect
Mark needs to find half the width of pieces of
pipe he is cutting to make a soccer goal. The width of the pipe is
3
inches. He wrote this equation to show the relationship between the
length and the width of the pieces he will cut. |
Every day that Cindy waters the garden, she earns
a dollar .She wrote this equation to show the relationship between
the number of days she waters the garden and the number of dollars she
will earn. |
Joe has one dollar in his wallet. He wrote this
equation to show the relationship between the number of dollars he
borrows from his friends for lunch and the total amount of money he has
or owes. |
Mia earns $2 for each magazines subscription sold
in the fund-raiser. A $1 fee per students is charged for a
processing fee. Mia wrote this equation to show the relationship between
the number of magazines sold and the profit. |
The flood waters are receding at a rate of q foot
per day .The river is currently at 1 foot above flood stage. Tom wrote
this equation to show the relationship between the number of days and
the height of the river compared to flood stage. |
Summary : Uses of Progress
Monitoring Data
• Estimate rates of student improvement
• Describe student response to instructional
program
• Inform teachers’ instructional decision making
• Aid teachers in targeting areas/skills that
need remediation
• Help teachers build potentially more effective
programs for particular students



