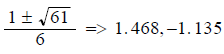First off, what does this equation thing look like?
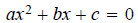
The x denotes that variable in the equation and while in this case it is
labeled x it could be
other letters as well.
The a,b, c are fixed real numbers and while in this case there is a+ before
the b and the c it
could just as well be a- .
These three numbers can be any number that you like with only 1 exception and
that is
a CANNOT be ZERO .
Examples
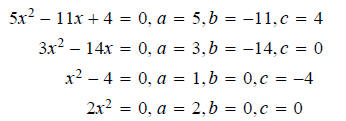
Where did these equations come from?
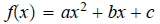
They came from a type of functions called quadratic functions which is part
of a larger
class called polynomial functions.
Quadratic functions look like a U that looks up (a>0) or looks down (a<0).
Example
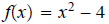
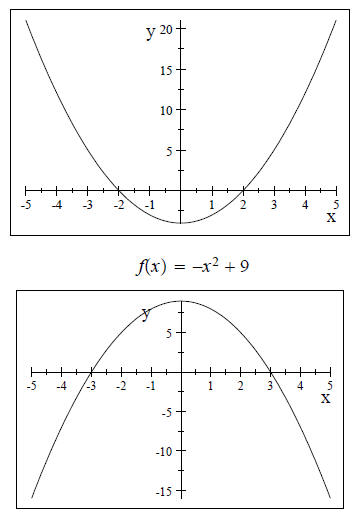
The reason that I brought this up is because our quadratic equation
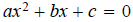
answers the question: Where does the quadratic function ( parabola ) cross on
the x axis or said
a different way where are the x intercepts?
There can be only 3 answers:
Crosses in 2 places, so 2 real number roots or solutions
Crosses in 1 place, so 2 real numbers roots that are repeated
Never crosses or touches x axis, so 2 complex number solutions
Recall
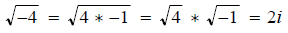
and if you forgot this do not panic, refer to section 0.8 in your text.
In this section we will see 4 ways to solve these equations
• By Factoring -> Easy but then again not many items factor
• By Square Root Property -> Requires a special format and is based on factoring
• By Completing the Square -> Long Process and simply converts quadratic
equation into
Square Root Property.
• By the Quadratic Formula -> Handy thing, always works, never leave home
without it.
Keep reminding yourself that factoring only works if you
have 0 on one side and
everything else on the other.
Square Root Property
This property says that if you can get your problem in the
format
(blob of symbols)^2=number
then you can conclude by factoring
blob of symbols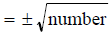 
Note
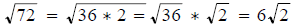
I am not picky about this and you can stop at square root
of 72.
Normally to get your answer you just use your calculator.
On Example 2 part b notice that it does not matter that
the number is -25, you just get
complex number solutions.
Completing the Square
The idea is to take
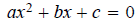
and turn it into
(blob of symbols)^2=number
1. Is a=1? If yes go to next step and if no then divide
all terms by a
2. Move the c term to RHS since it is in the way.
3. Record b=what?, Calculate 2 things
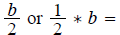Factor #, which we need
to save for factoring
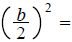Adding #, which we will
soon add to both sides
4. Add the Adding # to both sides
5. Combine the RHS and Factor the LHS (left hand side) always as (Equation
symbol followed by Factor # with its sign)^2
6. Solve using the Square Root Property.
Quadratic Formula
Page 114 derives the formula using Completing the Square.
Read through it but I will not
ask you to do it.
There are only a few things to comment on the formula:
1. Your problem must be in the standard format before you
can read off a, b, and c
2. -b really means -1 * whatever b happens to be
3. 4ac can turn out to be negative so make sure you do not lose track if you
have a double
negative.
4. b^2 − (4ac) is called the discriminant and its value positive , negative or
zero determines the
nature of your answers. This is shown on page 118.
What do I need for the test?
1. Solve an equation by factoring
2. Solve an equation by the square root property.
3. Solve an equation by completing the square.
4. Solve an equation by the quadratic formula and get the answers all the way to
simple
decimal answers using your calculator. For example you should be able to get the
2
decimal answers and not leave it in the format that they have
