Review of Matrix Algebra

2.1 Introduction
Before we begin our discussion of the statistical models and methods, we review elements of matrix
algebra that will be quite useful in streamlining our presentation and representing data. Here, we will
note some basic results and operations. Further results and definitions will be discussed as we need
them throughout the course. Many useful facts here are stated systematically in this chapter, thus, this
chapter will serve as a reference for later developments using matrix notation.

2.2 Matrix notation
MATRIX: A rectangular array of numbers, e.g.

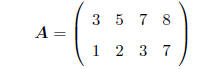
As is standard, we will use boldface capital letters to denote an entire matrix.

DIMENSION: A matrix with r rows and c columns is said to be of dimension (r × c).
It is customary to refer generically to the elements of a matrix by using 2 subscripts, e.g.

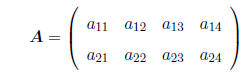
a₁₁ = 3, a₁₂ = 5, etc. In general, for a matrix with r rows and c columns, A, the element of A in the
ith row and the jth column is denoted as a_ij , where i = 1, : : : , r and j = 1, : : : , c.

VECTOR: A column vector is a matrix with only one column, e.g.

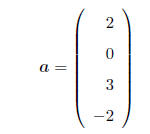
A row vector is matrix with only one row, e.g.

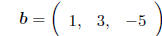
It is worth noting some special cases of matrices.

SQUARE MATRIX : A matrix with r = c, that is, with the same number of rows and columns is called
a square matrix. If a matrix A is square, the elements a_ii are said to lie on the (principal) diagonal
of A. For example,

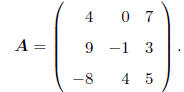
SYMMETRIC MATRIX: A square matrix A is called symmetric if a_ij = a_ji for all values of i and j.
The term symmetric refers to the fact that such a matrix "reflects" across its diagonal, e.g.

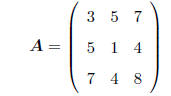
Symmetric matrices turn out to be quite important in formulating statistical models for all types of
data!

IDENTITY MATRIX: An important special case of a square, symmetric matrix is the identity matrix
-a square matrix with 1's on diagonal, 0's elsewhere, e.g.

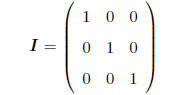
As we will see shortly, the identity matrix functions the same way as "1" does in the real number system.

TRANSPOSE: The transpose of any (r × c) A matrix is the (c × r) matrix denoted as A' such that
a_ij is replaced by a_ji everywhere. That is, the transpose of A is the matrix found by "flipping" the
matrix around, e.g.

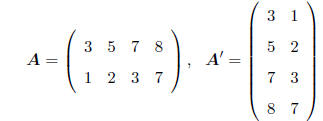
A fundamental property of a symmetric matrix is that the matrix and its transpose are the same, i.e.,
if A is symmetric then A = A'. (Try it on the symmetric matrix above.)

2.3 Matrix operations
The world of matrices can be thought of as an extension of the world of real (scalar) numbers. Just as
we add, subtract, multiply, and divide real numbers, we can do the same in with matrices. It turns out
that these operations make the expression of complicated calculations easy to talk about and express,
hiding all the details!

MATRIX ADDITION AND SUBTRACTION : Adding or subtracting two matrices are operations that
are defined element-by-element. That is, to add to matrices , add their corresponding elements, e.g.

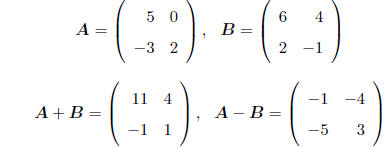
Note that these operations only make sense if the two matrices have the same dimension - the
operations are not defined otherwise.

MULTIPLICATION BY A CONSTANT : The effect of multiplying a matrix A of any dimension by a
real number (scalar) b, say, is to multiply each element in A by b. This is easy to see by considering
that this is just equivalent to adding A to itself b times . E.g.

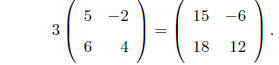
GENERAL FACTS:

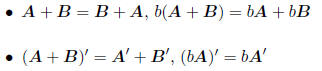
MATRIX MULTIPLICATION: This operation is a bit tricky, but as we will see in a moment, it proves
most powerful for expressing a whole series of calculations in a very simple way.

• Order matters
• Number of columns of first matrix must = Number of rows of second matrix, e.g.

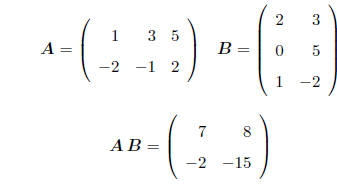
E.g. (1)(2) + (3)(0) + (5)(1) = 7 for the (1, 1) element.

• Two matrices satisfying these requirements are said to conform to multiplication.
• Formally, if A is (r × c) and B is (c × q), then AB is a (r × q) matrix with (i, j)th element

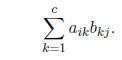
Here, we say that A is postmultiplied by B and, equivalently, that B is premultiplied by A .

EXAMPLE: Consider a simple linear regression model: suppose that we have n pairs (x₁, Y₁),....., (x_n, Y_n),
and we believe that, except for a random deviation, the relationship between the covariate x and the
response Y follows a straight line. That is, for j = 1,....., n, we have

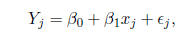
where 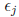is a random deviation representing the amount by which the actual observed response Y_j
deviates from the exact straight line relationship. Defining

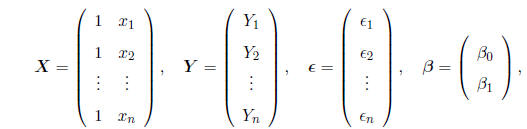
we may express the model succinctly as
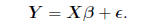(2.1)

SPECIAL CASE: Multiplying vectors. With a row vector premultiplying a column vector, the result is
a scalar (remember, a (1 × 1) matrix is just a real number!), e.g.

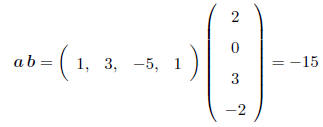
i.e. (1)(2) + (3)(0) + (-5)(3) + (1)(-2) = -15

With a column vector premultiplying a row vector, the result is a matrix. e.g.

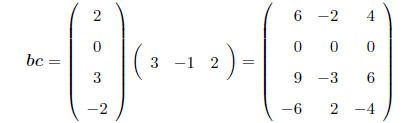
MULTIPLICATION BY AN IDENTITY MATRIX: Multiplying any matrix by an identity matrix of
appropriate dimension gives back the same matrix, e.g.

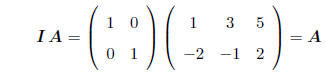
GENERAL FACTS:

• A(B + C) = AB + AC, (A + B)C = AC + BC
• For any matrix A, A'A will be a square matrix.
• The transpose of a matrix product - if A and B conform to multiplication, then the transpose
of their product
(AB)'= B'A':

These latter results may be proved generically, but you may convince yourself by working them out for
the matrices A and B given above.

LINEAR DEPENDENCE: This characteristic of a matrix is extremely important in that it describes
the nature and extent of the information contained in the matrix. Consider the matrix

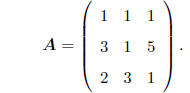
Refer to the columns as c₁, c₂, c₃. Note that
2c₁ + -c₂ + -c₃ = 0,

where 0 is a column of zeros (in this case, a (3 × 1) vector). Because the 3 columns of A may be
combined in a linear function to yield a vector of nothing but zeros, clearly, there is some kind of
relationship, or dependence, among the information in the columns. Put another way, it seems as
though there is some duplication of information in the columns.

In general, we say that k columns c₁₂, c₂,...., c_k of a matrix are linearly dependent if there exists a
set of scalar values 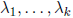such that
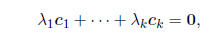(2.2)

and at least one of the 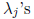is not equal to 0.

Linear dependence implies that each column vector is a combination of the others, e.g.,

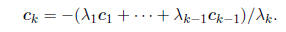
The implication is that all of the "information" in the matrix is contained in a subset of the columns
- if we know any (k - 1) columns, we know them all. This formalizes our notion of "duplication" of
information.

If, on the other hand, the only set of 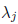values we can come up with to satisfy (2.2) is a set of all zeros,
then it must be that there is no relationship among the columns, e.g. they are "independent" in the
sense of containing no overlap of information. The formal term is linearly independent.