AN INTRODUCTION TO IRRATIONAL AND
IMAGINARY NUMBERS
Please note that the Texas Instrument TI 30X II B or TI
30X II S calculators will be used for all
calculator examples.
Review: Rational Numbers
Any type of number that can be written as the quotient of
two Integers. This includes all
terminating and repeating decimals, fractions , and the Integers.
Irrational Numbers
Any type of number that cannot be written as the quotient
of two Integers . They are non-terminating
decimal numbers.
Most irrational numbers result from findings roots of
certain other numbers. However,
there are also some irrational numbers that occur naturally, such as the number
π
(approximately 3.14) and the number e (approximately 2.72).
Real Numbers
The Real Numbers include all of the Rational and
Irrational Numbers.
Imaginary Numbers
Most imaginary numbers result from findings roots of
negative numbers given an EVEN
index only. The very basic imaginary number is given the letter i and i is
equal to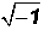 
There is no real number that can be squared to get a
result of -1. Therefore,
the solution to 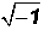only exists in our
imagination.
Please note that given an odd index, roots of negative
numbers result in rational or
irrational numbers.
Finding Irrational Numbers
Example 1 - Review of Unit 3:
Find the square root of 144.
According to the calculator
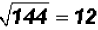, where 12 is a terminating decimal,
specifically
an integer, which is a rational number.
Remember that 12(12) does equal 144 !!!
Calculator Tip: You can find the square root in three
(3) different ways .
1. Easiest - Press the 2nd key and then the x^2 key.
Warning: Left parenthesis will open when you activate
, specifically
you will see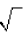 
( . After you type in the
radicand, you MUST type in the
right parenthesis, namely ")", before you press ENTER.
2. You might also remember from Unit 3 and Unit 4, that
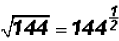. Therefore, you can
also use the following input
Warning: You must enclose 1/2 in parentheses to ensure
that the
radicand gets raised to the appropriate power ! See Order of Operation in
Unit 4.
3. You can also activate
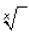to find the square root. Simply press the 2nd
key first
and then the carat key. Of course, you must remember that the index of a square
root is 2.
Warning: You first have to type the index, then press
the appropriate key
sequence, and then type in the radicand.
Example 2 - Review of Unit 7:
Find the cube root of -27.
According to the calculator
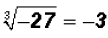, where -3 is a terminating decimal,
specifically
an integer, which is a rational number.
Remember that -3(-3)(-3) does equal -27 !!!
Calculator Tip: You might also remember from Unit 3 and
Unit 4, that
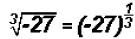. Therefore, you can
use the following input (easiest):
Warning: You must enclose both -27 and 1/3 in
parentheses. See Order
of Operation in Unit 4.
You can also activate
to find roots of any index. You have to
press the 2nd key
first and then the carat ^ key.
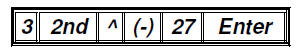
Warning: You first have to type the index, then press
the appropriate key
sequence, and then type in the radicand.
Example 3:
Find the cube root of 144.
Use the following easiest calculator input:
According to the calculator
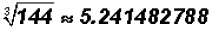, where 5.241482788 is a non-terminating
decimal, which is an irrational number.
We CANNOT find a number written as the quotient of two
integers that, when
cubed, results in 144.
Please note that the calculator eventually rounds to a
certain number of decimal
places. That does not mean that the decimal terminated.
Example 4:
Find the cube root of -7.
Use the following easiest calculator input:
According to the calculator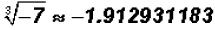
,where
-1.912931183 is a non-terminating
decimal, which is an irrational number. Note that the index is odd, therefore,
the root is NOT imaginary!
We CANNOT find a number written as the quotient of two
integers that, when
cubed, results in -7.
Example 5:
Given the number 81, find its square root, cube root, and
4th root.
square root: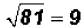 
... a
rational number (Unit 3)
because 9(9) = 81
cube root: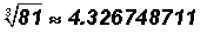 
... an
irrational number
We CANNOT find a number written as the quotient of
two integers that, when cubed, results in 81.
4th root: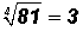 
... a
rational number (Unit 3)
because 3(3)(3)(3) = 81
Finding Imaginary Numbers
Example 1:
Find the square root of -81.
Use the following easiest calculator input:
The calculator tells us Domain Error!
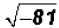is an imaginary number
because the INDEX IS EVEN and the radicand is
negative.
There is no real number that can be squared to get a
result of -81. Therefore,
the solution to 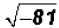only exists in our
imagination.
When we encounter the square root of a negative number,
it is customary to take
the negative sign out of the radicand and convert it to the letter "i" as
follows:
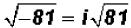. There is an
assumed multiplication sign between the number i and
the radical expression .
Since the number 81 is a perfect square , we can further
write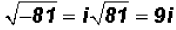 
.
It is customary to write the factor i AFTER a number once
the radical sign is eliminated.
Example 2:
Find the square root of -3.
Use the following easiest calculator input:
The calculator tells us Domain Error!
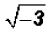is an imaginary number
because the INDEX IS EVEN and the radicand is negative.
There is no real number that can be squared to get a result of -3. Therefore,
the solution to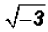 
only exists in our
imagination.
Again we finish by writing
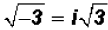. Sometimes, we want to change the radical
expression to a decimal approximation (remember it is a non-terminating decimal)
in which case we write
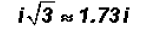
Remember that it is customary to write the factor i AFTER
a number once the radical sign
is eliminated .
Example 3:
Given the number -64, find its square root and cube root.
square root: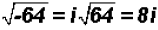 
... an
imaginary number (the index is even)
cube root: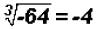 
... a
rational number (the index is odd)
because -4(-4)(-4) = -64
