The steps for simplifying in this section are to factor
then cancel . Given a rational
expression, the quotient of two polynomials , we will factor the numerator and
denominator if we can and cancel factors that are exactly the same.
When evaluating rational expressions we can plug in the
appropriate values either before
we simplify or after , the result will be the same. Although, it is more
efficient to simplify
first then evaluate.
We can see that when evaluating, the result will be the
same whether or not we simplify
first. It turns out that not all numbers can be used when we evaluate.
Evaluate 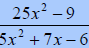 when when
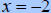 |
|
To find restrictions |
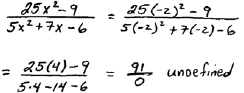  |
This indicates that we
have a restriction, or
that 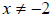 |
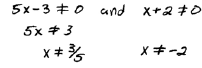 |
The point is that not all real numbers will be defined in
the above rational expression. In
fact there are two restrictions to the domain, x≠− 2 and
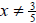 . These values , when
. These values , when
plugged in, will result in zero in the denominator . Another way to say this is
that the
domain consists of all real numbers except for −2 and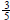 .
Tip: To find the restrictions,
.
Tip: To find the restrictions,
set each factor in the denominator “not equal” to zero and solve . The factors in
the
numerator do not contribute to the list of restrictions.
A. Simplify and state the restrictions to the domain.

Even if the factor cancels it still contributes to the
list of restrictions. Basically, it is
important to remember the domain of the original expression when simplifying.
Also, we
must use caution when simplifying, please do not try to take
obviously incorrect short cuts like this :


 |
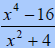 |
|
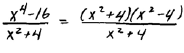
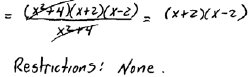 |
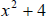 will never
will never
equal zero so there
are no real restrictions |
Since subtraction is not commutative we must be alert to
factors that are opposites. For
example notice that 5 – 3 = 2 and 3 – 5 = – 2. In general
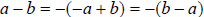 .
.
B. Simplify and state the restrictions to the domain.

At this point we will do the same type of problems using
function notation.
C. Simplify the function and evaluate.