Introduction
There are two kinds of finite element equation solvers : the direct and
iteration methods.
The direct method is based on the Gaussian elimination method , and its original
form was
modified by various ways to reduce the number of operations in computing , to
improve the
matrix condition number for accuracy, and to reduce the storage space of the
coefficient
matrix. Roughly speaking the total number of operations to finish up the
Gaussian
elimination procedure to solve a system of linear equations with n number of
equations, is
the order of n3 , that is, O(n3), while the required space to store the
coefficient matrix is
O(n2) if all of the coefficients are stored . If a coefficient is stored in 32
bit form, then we
need 64n2 bits space. In other words, if we have 20MB space for the coefficient
matrix,
then the largest n is about 790. This means that we can solve only 790
equations, and then
if a cubic hexagonal structure is modeled by 8 node slid brick elements, we can
only
decompose it into 5x5x5 meshes. This is not acceptable setting in practice. If
we have
20MB space for the coefficients, we would like to solve at least 10,000
equations. We can
find considerably many researches in the 1970s and 80s to reduce the storage
space
required. Typical outcome from such heavy research in the area of the finite
element
method and computational science, are, for example, the band method, skyline (
or profile )
method, wave front ( frontal ) method, and others. Especially, the wave front
method that
was developed by B. Iron was the highest achievement of the finite element
method in the
early 1970s. Because of this program to solve a system of linear equations that
is specially
designed by using the nature of linear elasticity, the finite element method
could attract wide
range people for its application, and we started solving “large scale” problems
with
O(1000) equations using 128K main memory computers with magnetic tape drives
which
provide leap frog type advancement in engineering analysis. He basically
developed an
algorithm which only requires storage of non- zero coefficients . It is noted that
the
coefficient matrix, that is the global stiffness matrix in the finite element
analysis, contains
mostly zeros. In other words, there are considerably less number of non-zero
terms than
zeros. Thus, as Iron developed, if we have an algorithm of the Gaussian
elimination
method which requires only non-zero terms, we can reduce large amount of storage
space
as well as computing time by skipping for zeros which do not make any influence.
After
Iron’s work, there were many modifications and variations, and then the skyline
( profile )
method became popular among researchers and students because of its simplicity.
A short
coming of the wave front method is its complexity of algorithm and programming,
although it was considerably simplified later, and it was applied by very
specialists of the
finite element method. On the other hand, the skyline method published in the
book by
Bathe was so simple that any engineering students could understand if they have
background of the Gaussian elimination method, and they could make their own
computer
programs without much effort. The skyline method requires more space than the
wave
front method, but it only requires storage of non-zero and zero terms bounded by
the socalled
skyline that is the most outer limit of non-zeros in columns of the coefficient
matrix.
It can be regarded as a variation of the band method that stores the non-zero
terms in a
rectangular matrix.
Direct Methods
The original Gaussian elimination method without pivoting
can be explained as follows.
Let a discrete finite element equation ( which is a typical matrix equation, and
represents a
system of linear equation with n number of unknowns and n number of equations )
:
Ax = b
or
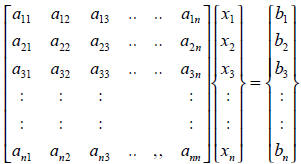
The first step is elimination of the terms
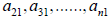of the first column using the first
row of the coefficient matrix A under the assumption that
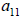is not equal to zero by using
the algorithm
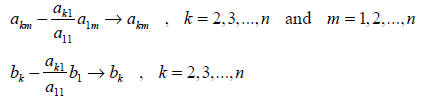
This operation leads the new matrix equation
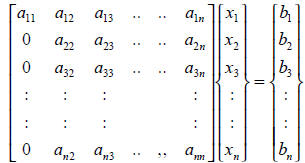
Here note that although we are using same characters
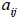with the original matrix equation,
their values are different since we replaced the original ones by the algorithm
described.
The next is to eliminate the terms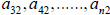 
of the
second column by the similar
algorithm
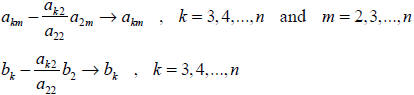
and obtain the new matrix equation
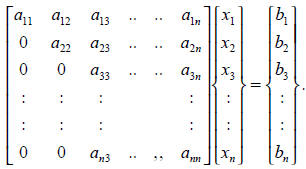
Repeat this process until the upper triangular coefficient
matrix is obtained :
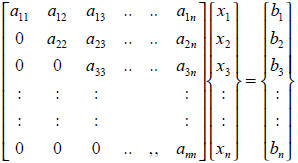
so that it can be solved from the last equation step by
step :
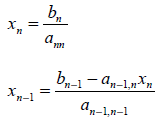
and
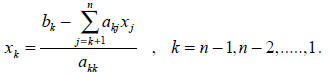
The process making the upper triangular coefficient matrix
is called the forward
elimination, the process modifying the right hand side is called the reduction,
and the last
step to solve the system linear equations with the upper triangular coefficient
matrix is
called the back substitution . If we examine this process, and if the coefficient
matrix has the
special structure such that all of non-zero terms are located within the band
from the
diagonals :
