Solving Linear Equations using Parallel Algorithms
| |
Overview
• Introduction
• Parallelization of Methods
– Direct (Gaussian Elimination + Back
Propagation)
– Iterative (Jacobi, Gauss-Seidel, Conjugate
Gradient)
• Applications |
Why important?
• Encounter linear equations when solving ODEs/PDEs
numerically .
• Many domains
– Structural Analysis (civil engineering)
– Heat Conduction & Fluid Dynamics (mechanical
engineering)
– Power Grid Analysis (electrical engineering)
– Regression Analysis (statistics)
|
Linear vs . Nonlinear Equations
• Linear system of equations 
• Non- linear system

|
Linear vs. Nonlinear Equations
• Navier-Stokes Equation for Compressible
Flow, a non-linear PDE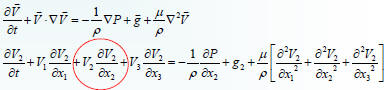
• With some assumptions for periodicity in
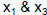 , it is reduced to a linear PDE , it is reduced to a linear PDE
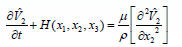 |
System of Equations
• General system with 4 unknowns
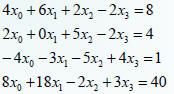
• Can obtain a system with finite differences
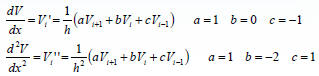
|
| System as a Matrix Equation
• Equation system as Matrix equation Ax=b

• Solve x =A-1b.
For dense systems we do
not solve by computing the inverse of A
directly, and for sparse systems we never
compute the inverse. |
Overview
• Introduction
• Methods and Parallelization
– Direct (Gaussian Elimination + Back
Propagation)
– Iterative (Jacobi, Gauss-Seidel, Conjugate
Gradient)
• Applications
|
Back Propagation
|
Back Propagation
How to parallelize?
• New
 values values
must be computed
sequentially
• Updating the
equations can be
done in parallel |
 |
|
Back Propagation
• Row-oriented parallel algorithm
– Each process gets a row of the
coefficient matrix and its
corresponding  value value
– Computation O(n2/p)
– Communication O(n log p )
|
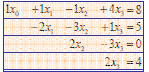 |
• Column-oriented parallel
algorithm
– Each process stores the
coefficients of a single 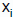 and and
entire b vector, and fires when
appropriate
– Computation O(n2) (no
computational concurrency)
– Communication O(n2) |
 |
|
Back Propagation
Which approach is better?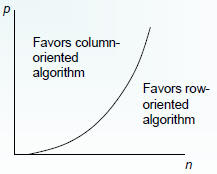
|
Gaussian Elimination
• How to get a dense matrix into the upper
triangular form for back-propagation?

|
Gaussian Elimination
• Robust implementation
includes row pivoting to
overcome roundoff errors
when dividing by small
coefficients
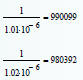
• Serial Pseudocode
– Choose pivot row O(n2)
– Perform elimination O (n3)
– Back substitution O (n2)
• Overall O(n3)
|
 |
|
Gaussian Elimination
• Parallelization – options for row
& column oriented approaches |
 |
• Tournament style evaluation to
determine pivot using
MPI_Allreduce with
MPI_MAXLOC |
• Elimination done in parallel
after divisor is broadcast |
• Use already developed parallel
back propagation algorithm |
| |
|
Gaussian Elimination
• Bad Decomposition Approach
– Row & Column Oriented give same time complexity ,
computation O(n3/p) and communication O(n2p log p)
– Poor Scalability, M = Cp(log p)2
– Poor because computation and communication are
done separately
• Good Decomposition Approach
– Pipelined row oriented algorithm, still computation
O(n3/p)
– Pivoting done column-wise, results sent in a ring
O(np)
– Overlaps communication and computation by forming
a ring, M = C and therefore scalable
|
Pipelined Gaussian Elimination
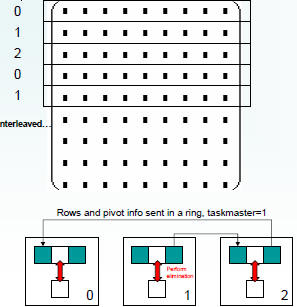 |
• Divide rows to processes
in an interleaved manner
• Each process gets the
current row used for
elimination and the pivot
column from the task
master at that iteration
• Elimination is performed,
and then the next process
in line becomes the task
master
|
|
Pipelined Gaussian Elimination
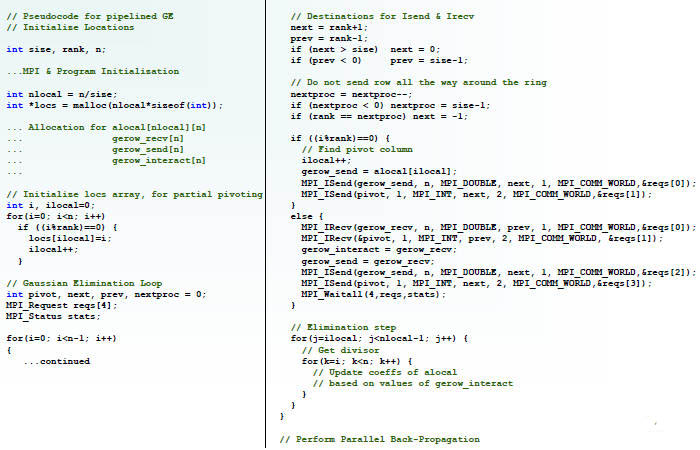 |
Start solving your Algebra Problems
in next 5 minutes!
 |
 |
 |
|
Algebra Helper
Download (and optional CD)
Only $39.99
|
|
Click to Buy Now:
OR
|
|
|
 |
 |
 |
|
2Checkout.com is an authorized reseller
of goods provided by Sofmath
|
|
Attention: We are
currently running a special promotional offer
for Algebra-Answer.com visitors -- if you order
Algebra Helper by midnight of
January 22nd
you will pay only $39.99
instead of our regular price of $74.99 -- this is $35 in
savings ! In order to take advantage of this
offer, you need to order by clicking on one of
the buttons on the left, not through our regular
order page.
If you order now you will also receive 30 minute live session from tutor.com for a 1$!
|
You Will Learn Algebra Better - Guaranteed!
Just take a look how incredibly simple Algebra Helper is:
Step 1
: Enter your homework problem in an easy WYSIWYG (What you see is what you get) algebra editor:
Step 2 :
Let Algebra Helper solve it:
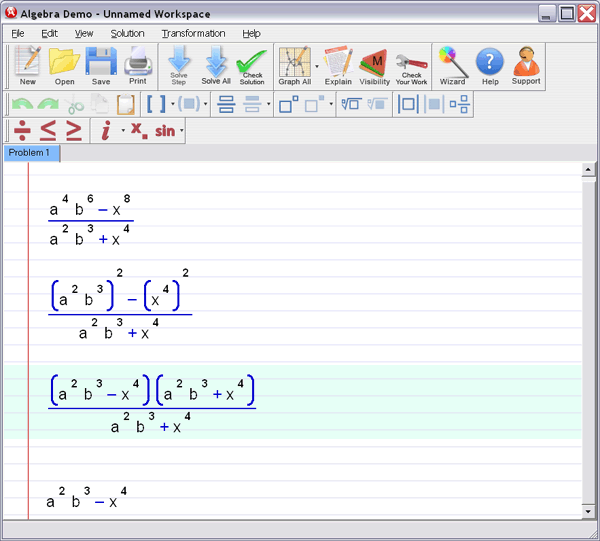
Step 3 : Ask for an explanation for the steps you don't understand:
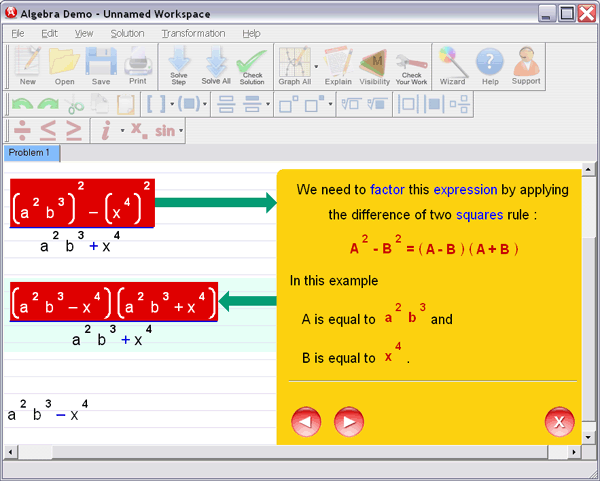
Algebra Helper can solve problems in all the following areas:
- simplification of algebraic expressions (operations
with polynomials (simplifying, degree, synthetic division...), exponential expressions, fractions and roots
(radicals), absolute values)
- factoring and expanding expressions
- finding LCM and GCF
-
(simplifying, rationalizing complex denominators...)
- solving linear, quadratic and many other equations
and inequalities
(including basic logarithmic and exponential equations)
- solving a system of two and three linear equations
(including Cramer's rule)
- graphing curves (lines, parabolas, hyperbolas, circles,
ellipses, equation and inequality solutions)
- graphing general functions
- operations with functions (composition, inverse, range, domain...)
- simplifying logarithms
- basic geometry and trigonometry
(similarity, calculating trig functions, right triangle...)
- arithmetic and other pre-algebra topics
(ratios, proportions, measurements...)
ORDER NOW!
 |
 |
 |
|
Algebra Helper
Download (and optional CD)
Only $39.99
|
|
Click to Buy Now:
OR
|
|
|
 |
 |
 |
|
2Checkout.com is an authorized reseller
of goods provided by Sofmath
|
|
|
 |
| |
| "It
really helped me with my homework. I was
stuck on some problems and your software walked me
step by step through the process..." |
| C. Sievert, KY
| |
| |
 |
| |
Sofmath
19179 Blanco #105-234
San Antonio, TX 78258
|
Phone:
(512) 788-5675
Fax: (512) 519-1805
| | |



