Properties of Integers : Divisibility, Primes, Euclid’s
Division Algorithm , Greatest Common Divisor (GCD), and Least Common Multiple
(LCM)
Recall the following definition of divisibility of
integers:
Definition: An integer a is divisible by integer b,
where b≠0, if a= bc for some integer c. In this case, b is called a divisor of
a; the notation is b| a. We often restricted the divisors to positive integers
since if b| a, where b≠0, then (–b) | a.
For example, since 12 = 3 ·4, we can say 3 | 12 (and 4 |
12). Also, 1 | n and n| n for any non- zero integer n.
Definition: An integer p is called a prime if p≥2,
and the only (positive) divisors of pare 1 and p itself; that is, if p is a
prime and a| p, where a> 0, then a= 1 or a= p.
Thus, some primes are 2, 3, 5, 7, 11, 13, …It is well
known that there exist infinitely many primes (proved by Euclid). However, it is
still unknown whether there are infinitely many prime pairs such as 3 and 5, 5
and 7, 11 and 13, etc., where two primes of the form p and p+2 (known as twin
primes). Any integer n > 1 can be factored into a product of primes in
essentially a unique way, which is known as the fundamental theorem of
arithmetic. It turns out that factorization is not a trivial problem; that is,
given a (large) integer finding its factors may take many steps given the
state-of-art algorithms. However, finding common factors between two integers
can be done very efficiently, something known to Euclid.
Definition: Given two positive integers a and b. An
integer m is a common divisor of a and b if m| a and m| b. The greatest common
divisor of a and b, denoted GCD (a, b), is the largest of the common divisors of
a and b. Note that the GCD always exists since 1 is always a common divisor, so
GCD (a, b) ≥1. Two integers a and bare relatively prime if GCD ( a, b) = 1.
We now develop Euclid’s algorithm which computes the GCD
of two positive integers. The basic idea is based on the following theorem.
Theorem: If a= bq+ r, where b ≠0, then GCD(a, b) =GCD(b,
r).
Proof: We first note that if m | a and m| b (that
is, if m is a common divisor of a and b), then m| r. This is true because m | a
implies a= mc; m | b implies b= md, for some integers c and d. Thus, r= a–b q=
mc –mdq= m(c –dq), which proves m| r. Thus, m is a common divisor of band r.
Therefore, m≤GCD(b, r) by the definition of GCD(b, r). In particular, GCD(a, b)
≤GCD(b, r). Similarly, we can prove that any common divisor of band r divides
a.. Thus, GCD(b, r) ≤GCD(a, b). Combining the two inequalities proves the
theorem.
Example: We now illustrate Euclid’s GCD algorithm
by computing GCD(228, 95).
228 = 95 •2 + 38, so GCD(228, 95) = GCD(95, 38).
Repeating the division process, using the previous divisor
and remainder as the dividend and divisor, respectively, of the next step, we
find
95 = 38 •2 + 19, so GCD(95, 38) = GCD(38,19); and since
38 = 19 •2 + 0, so GCD(38,19) = GCD(19, 0) = 19.
Combining, we find GCD(228, 95) = 19, the divisor of the
last division step.
Note that the above process always terminates since each
remainder is strictly smaller than the divisor of that step, thus strictly
smaller than the remainder of the previous step, so the remainder eventually
becomes zero. When that occurs, the last GCD between the divisor and zero is the
divisor itself, which gives the GCD of the original pair of integers.
Euclid’s algorithm written in C that computes the GCD is
given below:
int gcd (int a, int b) // assume a, b > 0
{ int r;
while (1) {// repeat until remainder = 0
r = a % b; // r is the remainder
if (r == 0) return b;
// otherwise
a = b; b = r;
}
} |
Theorem: Suppose a and bare two positive integers.
There exist integers t and u (may not be positive) such that at + bu = GCD(a,
b). That is, the GCD can be written as a linear combination of the two integers.
We will “demonstrate”this theorem by the extended Euclid’s
GCD algorithm. Basically, the GCD is equal to the remainder of the
second-to-the-last division step of Euclid ’s algorithm. Thus, the GCD can be
written as a linear combination of the dividend and the divisor of that division
step. We can then use the division step above it to substitute out its
remainder, resulting in a linear combination of the dividend and divisor from
this previous step. Repeating the substitutions using the division steps toward
the beginning of Euclid’s algorithm eventually leads to a linear combination in
terms of the original pairs of the integers.
Example. Find integers t and u such that GCD(228,
95) = 228 t + 95 u, that is, write GCD(228, 95) as a linear combination of 228
and 95.
Recall the following division steps in computing GCD(228,
95) using Euclid’s algorithm:
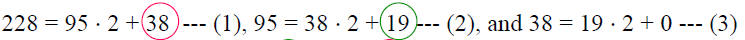
Thus, GCD(228, 95) = 19, and
 by rewriting the remainder in Step (2).We now substitute out the remainder
by rewriting the remainder in Step (2).We now substitute out the remainder
 from Step (1), thus, rewriting (4) as
from Step (1), thus, rewriting (4) as
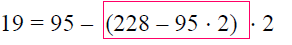
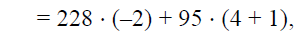 by
combining the like terms , writing as a linear combination of the previous
dividend and divisor
by
combining the like terms , writing as a linear combination of the previous
dividend and divisor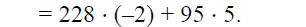
Thus, t = –2 and u= 5.
Theorem: If p is a prime and p| ab, then p| a or p|
b, where a and bare two positive integers.
Proof: Consider the value of GCD(p, a). Since this
is a divisor of p, but p is a prime by assumption, so GCD(p, a) = 1 or p (by the
definition primes). We now have two cases:
(Case one)
Suppose GCD(p, a) = 1. Write 1 = pt+ au using the Extended
Euclid’s algorithm. Multiplying both sides by b yields b= ptb+ abu= p(tb+ mu)
assuming ab= pm since p| ab by assumption. Thus, we proved p| b in this case,
(Case two)
Suppose GCD(p, a) = p. In this case, p is the GCD of p and
a, so p| a.
We can now state the following theorem which says any
integer greater than 1 can be factored into a product of primes , in essentially
a unique way. The proof is given on pages 3-6 and 3-7.
Theorem (Fundamental Theorem of Arithmetic ). Let
n≥2 denote an integer. Then there exists prime numbers
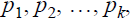 not necessarily distinct, such that
not necessarily distinct, such that
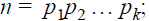 that is, any integer n≥2 can be factored as a product of prime numbers.
Furthermore, the product is unique except for possible rearrangement of the
prime factors.
that is, any integer n≥2 can be factored as a product of prime numbers.
Furthermore, the product is unique except for possible rearrangement of the
prime factors.
Example. Consider the following prime
factorizations:
10296 = 23•32•11 •13; 12675 = 3 •52 •132; and 25168 = 24•112•13.
Note that the GCD can be calculated quickly once the prime
factorizations are given. That is, if integers a and b have a common prime
factor p, e.g.,
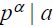 and
and
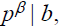 then
then
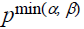 is a prime- power factor in GCD(a, b). Thus,
is a prime- power factor in GCD(a, b). Thus,
GCD(10296, 12675) = 3 •13 = 39; and GCD(10296, 25168) =
23•11 •13 = 1144.
Definition: The least common multiple of two
integers a and b, denoted LCM(a, b), is the smallest positive multiple of aand
b. For example, LCM(10296, 12675) = 23•32•52 •11 •132and LCM(10296, 25168) =
24•32•112•13.
Theorem: GCD(a, b) • LCM(a, b) = ab, for any
two positive integers a and b.
Proof: It can be seen that if
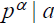 and
and
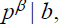 then
then
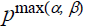 is a prime-power factor in LCM (a, b). Thus, the prime-power factor using prime
pin GCD(a, b) • LCM(a, b) is
is a prime-power factor in LCM (a, b). Thus, the prime-power factor using prime
pin GCD(a, b) • LCM(a, b) is
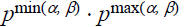 which equals
which equals
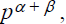 exactly the same as the prime-power factor using prime p in ab. Since this is
true for all prime-power factors of a and b, the theorem is proved.
exactly the same as the prime-power factor using prime p in ab. Since this is
true for all prime-power factors of a and b, the theorem is proved.



