Class time: Lectures: Mondays and Thursdays 9:20
p.m. - 10:50 p.m. in WIL/A120/H
Discussion section: Fridays 1.00 p.m. - 2.00 p.m. in PHY/C118/U
Text: David C. Lay, Linear Algebra and its
Applications
(updated second edition), Addison-Wesley-Longman, 1999.
Course Description: The course gives an
introduction to linear algebra and its applications.
This mathematical field is fundamental for a lot of other mathematical branches
and is highly
important in practice. The main topics include matrix algebra , solution of
linear equations ,
geometrical interpretations, vector spaces, determinants, eigenvalues and
eigenvectors, inner
products and orthogonality .
Exams and grading: There will be two in-class exams
during the semester, both during
normal class time. They will be held on May 2th and June 6th. The final exam
will take
place on July 7th. University policy states that you must take the final at the
scheduled time.
The attendance at lectures, discussion sessions and at all three exams is
required. Excuses for
missing a class are only acceptable if a written medical certificate or a
comparable document
is provided. In addition to the in -class exams, you will be required to submit
home work
once a week during the semester. This work will partially determine your
”discussion section
grade”. Each student has to give at least one presentation of an exercise in one
of the
discussion sections during the semester.
Grades for the course will be determined by applying the most favorable of the
following two
weighting schemes to your curved exam grades:
|
Scheme 1 |
|
Scheme 2 |
|
|
Your best in-class exam : |
25% |
Each in-class exam: |
25% |
|
Your other in-class exam: |
10% |
The final exam: |
35% |
|
The final exam: |
50% |
Homework and discussion sections: |
15% |
|
Homework and discussion sections: |
15% |
|
|
Homework: At the end of thursday’s lecture you will
get exercises related to the subjects
discussed in the classes of that week. You will be expected to submit your
homework until
monday next week.
Summary of the subjects of the lecture:
1. Matrix Algebra
2. Solving Linear Equations
3. Geometric Description of 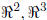
4. Vector Spaces
5. Orthogonality
6. Eigenvalues and Eigenvectors
7. Minimization Problems, Constraint Optimization
Time schedule and correlation of the subjects to the sections of the book:
| |
Time |
Lecture |
Section |
Discussion |
1
|
04/04/05
07/04/05 |
Introduction, examples, Matrix- Vector operations
Matrix operations |
I.3-4
II.1 |
08/04/05 |
2
|
11/04/05
14/04/05 |
Specific Matrices, The Inverse matrix
Procedure for solving linear equations , Echelon forms |
II.2
I.1-2 |
13/04/05 |
3
|
18/04/05
21/04/05 |
Solution sets, Computing the inverse, an example
LU- Factorization |
I.5, II.2
II.5 |
20/04/05 |
4
|
25/04/05
28/04/05 |
Iterative solving, Partitioned matrices
Geometric description of 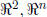 , Linear
transformations , Linear
transformations |
II.6. II.4
I.3, I.7 |
27/04/05 |
5
|
02/05/05
05/05/05 |
In class Exam I
Holiday: Himmelfahrt |
|
04/05/05 |
6
|
09/05/05
12/05/05 |
Vector spaces: basic notations and examples
Dies Academicus |
IV.1, 3-6 |
11/05/05 |
7
|
16/05/05
19/05/05 |
Holiday
Holiday |
|
|
8
|
23/05/05
26/05/05 |
Inner product, Orthogonality
Orthogonal projections, The Gram-Schmidt Process |
VI.1,VI.7
VI.2-3 |
25/05/05 |
9
|
30/05/05
02/06/05 |
Matrix notation in vector spaces
The Determinant |
IV.2
III.1-3 |
01/06/05 |
10
|
06/06/05
09/06/05 |
Applications
Eigenvalues and Eigenvectors |
IV.6-9
V.1 |
8/06/05 |
| 11 |
13/06/05
16/06/05 |
In class Exam II
The characteristic equation , Diagonalization |
V.2-3 |
15/06/05 |
12
|
20/06/05
23/06/05 |
Jordan normal form, Singular value decomposition
Applications |
V.3, VII.4 |
22/06/05 |
13
|
27/06/05
30/06/05 |
Symmetric matrices
Minimization problems, Least Squares method |
VII.1
VI.5 |
29/06/05 |
14
|
04/07/05
07/07/05 |
Applications to practical problems
Final Exam |
VI.6 |
06/07/05 |
15
|
11/07/05
14/07/05 |
Some aspects of constrained optimization
Some resume & Conclusions |
VII.2-3 |
13/07/05 |



