Special Polynomials
Patterns
Certain polynomials can be factored by finding a pattern . This section deals
with four special
patterns for factoring polynomials: difference of squares , difference of cubes,
sum of cubes, and
perfect squares
Difference of Squares
The difference of squares pattern can be identified by looking at the
polynomial. It must be a
binomial, the first term must be a variable to the second power (a.k.a. squared)
and a constant
term must be subtracted from it. There is no first- order variable term in a
difference-of-squares
polynomial. The formula a^2 - b^2 = (a - b)(a + b) is how a difference of
squares polynomial is
factored.
Example: Factor x^2 – 25.
This binomial has its first term is x^2, a second-order monomial. The only other
term is 25,
just a constant. This means x^2 – 25 can be factored using the difference of
squares pattern, so
x^2 – 25 = (x)^2 – (5)^2 = (x – 5)(x + 5).
To check, we can multiply the factored form back together using the FOIL method :
(x – 5)(x + 5) = x^2 + 5x – 5x – 25 = x^2 – 25.
Example: Factor 9x^2 – 36.
This binomial’s highest order monomial is 9x^2; the other monomial is the
constant 36, so we
can factor 9x^2 – 36 using the difference of squares method: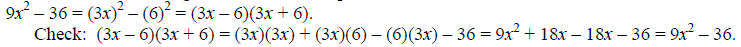
Note: There is no sum of squares factorization; that is,
we can’t factor a^2 + b^2.
Difference of Cubes
To find the pattern for the difference of cubes, the polynomial to factor must
be a binomial, the
first term must be a variable to the third power (a.k.a. cubed) and a constant
term must be
subtracted from it. There cannot be any first- or second-order variable terms in
a difference-of-cubes
polynomial. The formula a^3 - b^3 = (a - b)(a^2 + ab + b^2 ) is the
factorization of a
difference-of-squares polynomial.
Example: Factor the binomial 8x^3 − 1.
This binomial has 8x^3, a third-degree term, as its highest- powered monomial and
only a
constant, 1, is subtracted from it. We can factor by using the difference of
cubes formula :
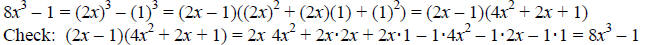
Example: Factor the polynomial b^3 – 64.
The highest degree in this binomial is 3, on the b^3 term. The only other
monomial in the
binomial is 64, so the difference of cubes form is useful for factoring:
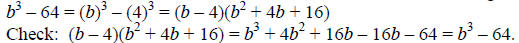
Sum of Cubes
A sum of cubes polynomial is similar to the difference of cubes polynomial,
except that the
constant term is added to the third -order monomial instead of subtracted. The
formula for the
factoring pattern is a^3 + b^3 = (a + b)(a^2 - ab + b^2 ) .
Example: Factor the binomial a^3 + 125.
This binomial is a cubic monomial (a^3) plus a constant (125) so we can use the
formula:
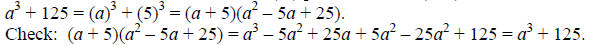
Example: Factor x^3 + 27y^3.
This binomial is a cubic monomial plus another cubic monomial, so we can use the
formula:
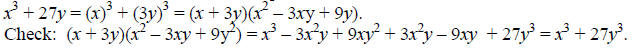
Perfect Square Trinomials
There are two patterns for the perfect square trinomial: x^2 + 2xy + y^2 = (x +
y)^2 and
x^2 - 2xy + y^2 = (x - y)^2 . This trinomial has three terms: two of the terms
(usually the first and
last) are monomials that we can easily take the square root of , and a third term
is twice the roots
of the other two terms multiplied together. Note that only the sign of the
middle term can be
positive or negative , and it matches the sign in the middle of the factored
form. All of the other
coefficients must be positive.
Example: Factor x^2 – 4x + 4
This is an example of a perfect square trinomial: it is easy to take the square
root of the first
and last terms (x^2 and 4), and the middle term is twice the roots of the end
terms. We can use the
formula. Since the middle term is negative, we will subtract the two terms in
the formula:
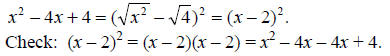
Example: Factor the trinomial 25x^2 + 80x + 64
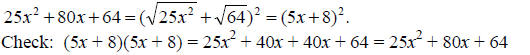
1. Factor 4x^2 – 16.
Difference of squares
4x^2 – 16 = (2x + 4)(2x – 4)
2. Factor 81x^2 – 49.
Difference of squares
81x^2 – 49 = (9x + 7)(9x – 7)
3. Factor 100a^2 – 16b^2
Difference of squares
100a^2 – 16b^2 = (10a + 4b)(10a – 4b)
4. 125y^3 – 64
Difference of cubes
125y^3 – 64 = (5y – 4)(25y^2 + 20y + 16)
5. b^3 – 8a^3
Difference of cubes
b^3 – 8a^3 = (b – 2a)(b^2 + 2ab + 4a^2)
6. a^3 – 27y^3
Difference of cubes
a^3 – 27y^3 = (a – 3y)(a^2 + 3ay + 9y^2)
7. 64x^3 + 27
Sum of cubes
64x^3 + 27 = (4x + 3)(16x^2 – 12x + 9)
8. 125z^3 + 1
Sum of cubes
125z^3 + 1 = (5z + 1)(25z^2 – 5z + 1)
9. 4x^2 + 36x + 81
Perfect square trinomial
4x^2 + 36x + 81 = (2x + 9)^2
10. x^2 + 2x + 1
Perfect square trinomial
x^2 + 2x + 1 = (x + 1)^2



