Class outline
1 Old Business
1 exam and homework
2 inequalities
2 New Business
1 Why study quadratics
2 equations from geometry
3 functions from physics
4 Where do higher degree polynomials come from?
5 Solving quadratic equations
Exam
A: > 90
B: 80 < x ≤ 90
C: 70 < x ≤ 80
problem 6:
Linear regression on dog walk ?????
What is a piece of a function?
And versus Or
Suppose A and B are two statements .
When is A and B true?
When is A or B true?
Suppose A and B are two statements.
When is A and B true?
When is A or B true?
A and B is true exactly when both are true.
A or B is true exactly when at least one of them is true.
inclusive or.
Solutions of Absolute Value Inequalities
|x| < a means
x < a AND x > −a.
|x| < a means
x < a AND x > −a.
|x| > a means
x > a OR x < −a.
Examples
|3x − 2| < 7
|4 − 5x| ≥15
| − 3x| = −1
Graphical Methods : Example
Example of the split point method: To solve |3x − 2| < 7 by
the split point method, graph the two functions y = |3x − 2|
and y = 7. The solution is the set of numbers on the real line
such the value of the first function is less than the value of the
second.
The real axis is divided into a finite number of intervals by
those x where the lines cross. These are called split points.
(In this example the intervals are
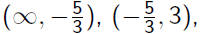 and
and
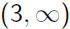 .
The middle one is where the inequality holds .)
.
The middle one is where the inequality holds .)
Graphical Methods: General case
Let f and g be polynomials.
To solve: f (x) < g(x).
Graph the two functions. They will cross at finitely many
points ai where f (ai) = g(ai).
These are the split points. The solutions are the intervals
determined by these split points where the inequality holds.
Two kinds of problems
1. inequalities in one variable. The solution is a union of
intervals in the real line – a set of numbers.
2. inequalities in two variable. The solution is a set of points in
the plane. The solution will be a shaded set of point in the
plane.
Find the form |x − a| < b
Suppose we are looking at {x : −2 < x < 10}.
|x − 4| < 6
|x − a| < b
a midpoint of the interval; b is 1/2 of the length.
Graphs I
Discuss problems 3, 4, 5 from the interpreting graphs
homework.
Velocity versus speed.
Why study quadratics
1 Equations:
A rectangle is two feet longer than it is wide. If the area of
the rectangle is one square foot , what are the dimensions
of the rectangle?
Functions: A ten pound weight is dropped from the
leaning tower of Pisa. After 9.3 seconds it hits the ground.
How fast is it going when it hits? How high is the Leaning
tower of Pisa?
Distance = rate times time
What does this mean?
constant rate
Acceleration
A ball rolls down a ramp with a constant acceleration of 4 ft.
per second squared.
What is its velocity after 1 second, 2 seconds etc.
How far has it traveled after 1 second, 2 seconds etc. ?
velocity = acceleration times time
consider examples.
v = at
What was the average velocity?
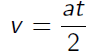
Why? Velocity at beginning is 0. Velocity at end is at.
So the average is
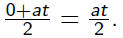
What is the area under the line?
distance
Constant acceleration; initial velocity 0:
d = rt
So we use the average velocity we computed on the previous
slide as if it were a constant velocity for the problem.
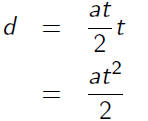
Example
A ball rolls down a ramp with a constant acceleration of 6 ft.
per second squared.
a) What is its velocity after 5 seconds?
b) How far does it travel in 5 seconds?
A ball rolls down a ramp with a constant acceleration of 6 ft.
per second squared.
a) What is its velocity after 5 seconds?
b) How far does it travel in 5 seconds?
c) If the ramp is 10 feet long, when does the ball reach the
bottom of the ramp?
Solution
a) v = at, so v = 6 × 5; 30 feet per second.
b) The average velocity is the final velocity over two: 15 feet
per second. So the distance traveled is 15 × 5; 75 feet.
c)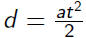 and
a = 6 while d = 10. So
and
a = 6 while d = 10. So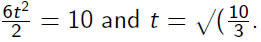
Some terminology
A monomial is a product of numbers and variables.
e.g.
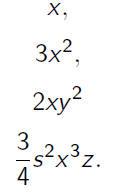
A monomial is a product of numbers and variables.
e.g.
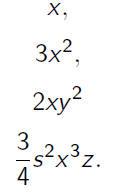
A polynomial is a sum of monomials .
binomial, trinomial
multiplying polynomials
What is
(a + b)(c + d)?
What is
(a + b)(c + d)?
What is
(a + b)(c + d + e)?
Multiplying binomials
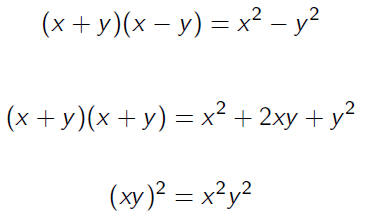
Algebra and Arithmetic
Multiply in your head. 18*22, 99*101, 402, 41*39.



