Math Test

Varsity Ciphering 2007

Round 1

1. Find the distance from R(6, -4) to the line with the equation y = 12.

2. Solve 2cos²x+cosx=1 for 0 ≤ x < 2π.

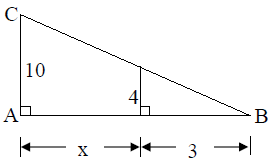
3. Shown in the figure is a right triangle ABC with line segments with the indicated measures. Find the value of x . Express the answer as a reduced fraction.

4. If 100×19.98×1.998×1000=x² find x for x > 0.

5. The length of one side of an equilateral triangle is 4 centimeters. Find the length of an altitude of the triangle.

6. Simplify the following : (x^-1+y^-1)/(x^-1−y^-1). Leave no negative exponents nor complex fractions.

7. State the period of y=1/2 tan 8x.

8. If @ is defined for all positive numbers a and b by  a@b = 5−2ab−b² find 5 @ 2.

Round 2

1. Find the value of “k” so that the slope of the line through the points (5, k) and (9, 4) is 3/2.

2. Solve 2sinx+1=0 on the interval [0,2π).

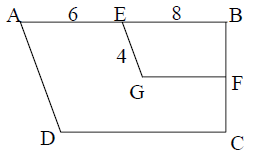
3.Shown in the figure are similar trapezoids ABCD and EBFG with line segment measures as indicated. Find the measure of AD.

4. An island has no currency, instead it has the following exchange rate:
50 bananas = 20 coconuts
30 coconuts = 12 fish
100 fish = 1 hammock
How many bananas equal 1 hammock?

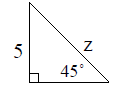
5. In the triangle shown with the indicated measures find the value of z .

6. Solve the following : .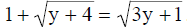

7. Starting from the origin and for x ≥ 0 in radians what are the coordinates of first occurrence of the maximum point of the graph of ? y=−2cos2x

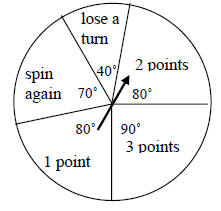
8. The spinner shown is a circle subdivided into sectors with central angles as shown. Find the probability that the spinner will land on “lose a turn”.

Varsity Ciphering 2007 Answers

Round 1

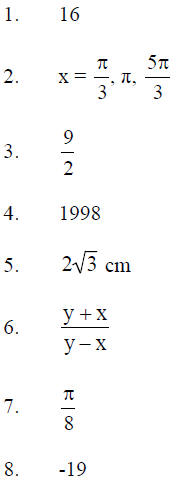
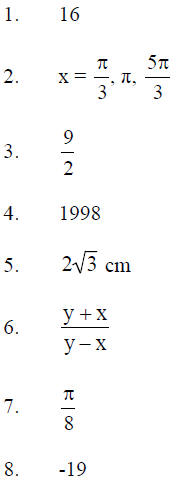
Round 2