Given a system of equations
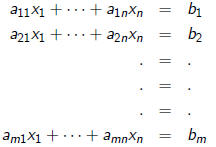
Write down the augmented matrix which is just a array of
numbers
representing the equations .

Using Row operations reduce it to echelon form

We will formalize this later. Let us do another example.
Let us say we want to find the plane that passes through
the set of vectors
(0, 1,-1), (1, 1,-2), (2,-1, 1).
Equation of a plane is given by
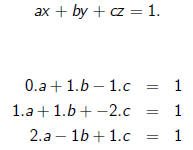
What is the augmented matrix representing this system of equations ?
What are row operations ?
•Exchanging rows
• Multiplying a row by a fixed number
• Adding rows
What are row operations really ?
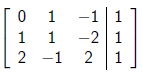
to
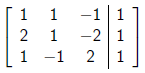
Can I do this ?
or transform to ?
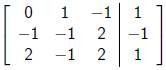
The first non zero entry in a row is called the pivot.
Definition
Matrix is in a Row Reduced Echelon form if
•Pivot entry is 1.
•If a column has pivot entry then all the other entries are zero .
•If a row has a pivot then rows above it contain pivots in columns left to that.
The process of using row operations to get an augmented matrix into Row
Echelon form is called Gauss Jordan Method .
A matrix is just an array of numbers arranged in rows and columns.
How do matrices represent vectors?
Given an m*n matrix what are the row vectors?
What are the column vectors?
Definition
A 1*n matrix is called a row vector.
A m*1 matrix is called a column vector. We will define Rn to be the set
of all column vectors.
We are just setting convention that vectors mean column
vectors.
Consider this augmented matrix
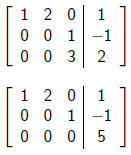
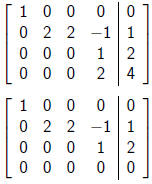
Does a system of equations always have a solution ?
Can you come up with some criteria?
• solving system of equations
•Gauss Jordan Method
•Row echelon form
•Vectors