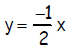1. The exam covers Sections
3.3-3.8, 4.1-4.5. The exam will be closed book, closed notes, and turned off
cell phones. Calculators are allowed .
2. Practice doing problems without using the
book or your notes. I will only test you on ideas that we have covered in class
and on your homework.
3. Review the topics and do the problems
listed below. Review homework and in-class worksheets. If a certain problem type
is difficult for you, do some other problems like it in the book for more
practice.
4. Do not wait until the night before the
exam to begin studying.
5. Make sure to show all your work.
6. Do not skip an exam. Check my syllabus for
exam policy.
Fraction Review
Add , subtract , multiply, divide fractions and
mixed numbers:
1.
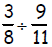
2.
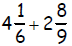
3.
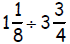
Solve Linear Equations
Solve linear equations :
4. -3x - 17 + 4x = 5
5. 2(2x - 5) = 3(x + 4)
6.
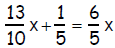
Section 3.3
Solve a formula for the specified variable :
7. 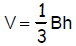 for h
for h
8. P = 2L + 2W for L
9. ax + by + c = 0 for x
Solve for y; put the resulting equation into
y = mx + b form:
10. 2x + 5y = 10
11. 3x = 4y + 11
12. 3x - y = 5x + 3y
Section 3.4 and 3.5
Solve application problems: set up a
variable, write an equation, solve the equation, and then
answer the question.
13. A 6 foot board is cut into 2 pieces so
one piece is 2 feet longer than 3 times the shorter piece. If the shorter piece
is x feet long, find the lengths of both pieces.
14. For a four number lottery , a person's
first three picks were consecutive odd integers, and the fourth was the sum of
the first three numbers. If the fourth number was 45, what are the first three
numbers.
15. One angle of a triangular banner is 20
degrees greater than the first angle. The third angle is twice as large as the
first angle. What are the measures of the three angles?
16. How much pure acid (100%) should be mixed
with 2 gallons of a 50% acid solution in order to get an 80% acid solution.
17. The owners of a candy store want to sell,
for $6 per pound, a mixture of chocolate-covered raisins, which usually sells
for $3 per pound, and macadamia nuts, which usually sells for $8 per pound. They
have a 60-pound barrel of the raisins. How many pounds of the nuts should they
mix with the barrel of raisins so they hit their target value of $6 per pound
for the mixture?
Section 3.6 and 3.7
Solve
inequalities and compound inequalities. Graph the
solution set AND write it in interval notation.
18. 7x + 1 ≥15
19. 5 -y > 0
20. 3 -2x ≥-2x + 1
21. 2x + 7 < 3 + 5x
22. 3(x + 4) > 2x -3
23. -2x + 18≤-2(5x ?3)
*24. - 7≤-2x + 3 < -3
25. x -2 > 3 and x -5 < 4
26. 2x + 3 ≥-1 and 3x + 6 < 21
27. -x -5 > 0 or 3x -2 ≥1
28. -x -6 ≥3 or 4x + 3 > 5
Section 3.8: *BONUS MATERIAL
Solve basic absolute value equations; graph
basic absolute value inequalities.
(We will go over these in class on the review
day.)
*29.
| x |
+ 2 = 5
*30. |
x | ≥2
*31. |
x | ≤7
Sections 4.1, 4.2, and 4.3
1. Find slopes of given lines.
2. Determine the slope and y- intercept of
given equations.
3. Determine if lines are parallel,
perpendicular or neither.
4. Graph equations.
32. Complete the ordered pair so that it is a
true solution of the given linear equation:
3x + y = 2 ( ___, 8 ), ( ___, -4 ), ( 0, ___)
Write each equation in slope intercept form
and determine the slope and y-intercept:
33. 2x + 3y = 14 34.
13x+34y-9=0
Determine the slopes of the given equations:
35. 3x = 12
36.-y = -8
Two points of two lines are given; determine
if the lines are parallel, perpendicular, or neither.
37.
L
1: (3, 5)
and (-2, 1)
L2:
(-6, 9) and (-1, 13)
38.
L1: (4, 8)
and (1, -2)
L2:
(-3, 5) and (2, 2)
The equations of two lines are given;
determine if the lines are parallel, perpendicular, or neither.
39.
L1: 3y = 5
-2x
L2: y = 3/2x + 9
40.
L1: y = 5x -3
L2:
y = -5x + 3
Use the slope-intercept form to graph the
equations:
41. y = -4x -7
42. 5x + 4y = 20 43. x -3 = 4
44. y = -3x + 4
45. x + 3y -y = 0
Section 4.4
Write equations in slope-intercept form given information.
Try problems like:
Write the equation of the line in
slope-intercept form given the following information.
46. m = - 3, (2, 5)
47. m = -1/3, (-6, 3)
48. m is undefined, (6, 8)
49. m is zero , (6, 8)
50. (4, 7) and (6, 11)
51. (4, 0) and (2, 5)
Section 4.5
1. Graph linear inequalities.
2. Graph compound linear inequalities.
Try problems like:
52. y ≤1/2x -5
53. 4x + 5y > 20
54. 2x -5y ≥10
55. y ≤-x + 3 and y ≤2x + 1
56. -x + 4y < 12 or x ≥2
Solutions:
Fraction Review:
1. 11/24
2. 7 1/18
3. 3/10
Solve Linear Equations:
4. x = 22 5. x = 22 6. x = -2
Section 3.3:
7. 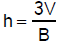
8.
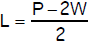
9.
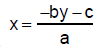
10.
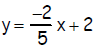
11.
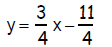
12.