Functions

Solutions to Exercises

2.41. Solution of (a). Is y a function of x? Yes.

Indeed, take the given equation 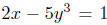and solve, if possible,
for y. We get

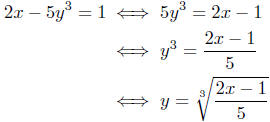
Thus, for each value of x there is only one corresponding value of y.
We could name this function as 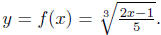It is easy to see
that the natural domain is Dom(f) = R.

Important Fact. (The Existence and Uniqueness of Odd Roots) The
pivotal fact used in this calculation is that any real number has a
unique real cube root . More generally, if n ∈ N is an odd natural
number and z ∈ R is any real number, then 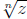exists as a real
number and is unique. What this means in terms of solving equations
is

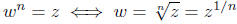n odd

Solution to (b): Is x a function of y? Yes.

Take the equation 2x - 5y³ = 1 and try to write x in terms of y:

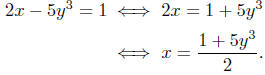
These calculations justifies the conclusion. Each value of y determines
only one corresponding value of x. Let's name this function

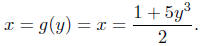
It is easy to see that Dom(g) = R is the natural domain of g.
Exercise 2.41.

2.42. (a) Yes. (b) No.

Solution to (a): Is s a function of t?

Try to solve for s in terms of t. (Why?)

That was simple. Thus, each value of t yields only one value of s; s is
indeed a function of t. We can use the notation

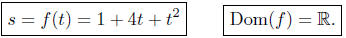
Solution to (b): Is t a function of s?

Try to solve for t in terms of s. (Why?)

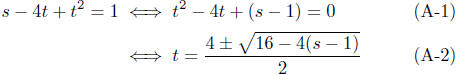
This shows that for each value of s (for which the radicand is nonnegative)
there is two value of t. Thus, t is not a function of s.

Example Notes. In line (A-2) we used the infamous quadratic formula.
The solution to the equation

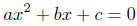
is

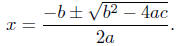
This is why I set up the equation in line (A-1). Exercise 2.42.

2.43. (a) No. (b) No.

Solution to (a): Is x a function of m?

I need to find the x-coordinate(s) of the point(s) of intersection between
the line y = mx and the circle x² + y² = 1.

At any point of intersection ( x, y ), the two variables satisfy both
equations simultaneously : If ( x, y ) is a point of intersection then

y = mx and x² + y² = 1.

Thus,

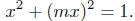
Now, solving this last equation for x gives the x-coordinate(s) of the
point(s) of intersection.

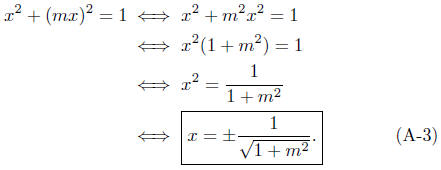
Equation (A-3) indicates to me that x is not a function of m: Each
value of m yields two values of x.

Solution to (b): Is m a function of x?

Given that x is the x-coordinate of the point(s) of intersection between
the circle x² + y² = 1 and any line of the form y = mx, we must
determine the value of m.

Just as in part (a) we have x² +(mx)² = 1, but now we want to solve
for m in terms of x (Why?)

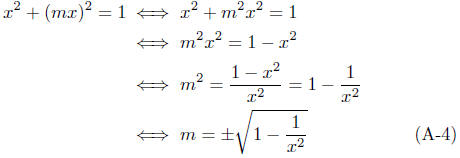
This shows that form each x, x ≠ 0, -1≤ x ≤1, there corresponds
two values of m. This means that m is not a function of x.

Example Notes: I assume you have drawn a picture of the described
situation. The two algebraic solutions were more difficult than merely
looking at the picture of the situation and reaching the proper conclusions
based on your understanding of the concepts. Equally well, it
is obvious, geometrically, why x ≠ 0 in (A-4): When x is zero, there
is no corresponding m at all; for in that case the corresponding line
is vertical, the slope of a vertical line is undefined. Exercise 2.43.

2.44. I cannot justify it in your own mind, only in mine.
Exercise 2.44.

2.45. Perhaps one could call this the horizontal line test?

A curve C in the xy -plane defines x as a function of y if it is true that every horizontal line intersects the curve at no more than one point.

If this be true, then for each y there corresponds at most one x -
this is descriptive of the concept of x is a function of y. (Note: if for a
given y the horizontal line at altitude y does not intersect the curve,
this means that y does not belong to the domain of the function.)
Exercise 2.45.

2.46. Simply restate the Function Line Test using these different
letters:

Solution to (a): C defines s as a function of t provided every line
perpendicular to the t-axis intersects the curve at no more than one
point.

Solution to (b): C defines t as a function of s provided every line
perpendicular to the s-axis intersects the curve at no more than one
point .Exercise 2.46.

2.47. Let C be a curve in the pq-plane.

Under what conditions can we assert that p is a function of q? Review
the definition of function in your head, and answer this question
without error. Passing Score. 1 out of 1.

(a) Every line perpendicular to
the p-axis intersects the curve
at no more than one point.

(b) Every line perpendicular to
the q-axis intersects the curve
at no more than one point.
Exercise 2.47.

4.1. Yes.

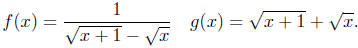
Domains Equal? We must have x+1 ≥0 and x ≥0 for the radicals
in the two functions to be real numbers. The next question, is whether
the denominator of f can ever be zero ; indeed,

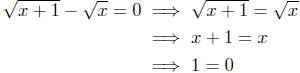
We have argued that if 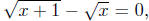then 1 = 0; therefore, we
conclude 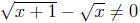for any x ∈ R.

The domains of these two functions requires x + 1 ≥0 and x ≥0;
therefore,

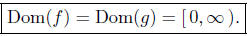
Pointwise Equal? Suppose x ∈ Dom(f) = Dom(g), then

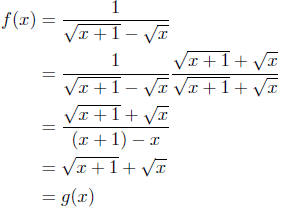
Thus,

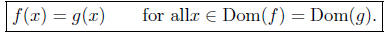
Conclusion: Yes indeed, f = g.

Example Notes: You did remember the trick of multiplying by the
conjugate, didn't you? It is also important to note that the quantity
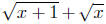is never equal to zero; therefore, multiplying the numerator
and denominator by this quantity is equivalent to multiplying by
one, no matter what the value of x. Exercise 4.1.

4.2. No. Recall,

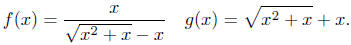
Domains Equal? I think we can take a useful shortcut. Note that
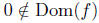since x = 0 makes the denominator equal to zero (and the
numerator too ). But 0 ∈ Dom(g) since we can calculate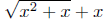
for the case of x = 0; indeed, g(0) = 0. Thus, we have argued that
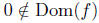and 0 ∈ Dom(g). Therefore,

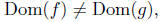
and so,

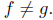
All done!

Exercise Notes: However, we can say 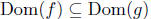and that for
all 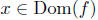we have f(x) = g(x). In this case, we say that g is an
extension of f. Exercise 4.2.

4.3. Look at the calculating formula. The concept is to add the values
of f and g together. So given an x, we need to have defined the value
f(x). This implies x∈ Dom(f). Similarly, we need to add f(x) to g(x)
-g(x) needs to be a defined quantity; therefore, x ∈ Dom(g) as well.
We have argued that in order to carry out the concept of summing
two functions together, we must choose an x in both Dom(f) and in
Dom(g). Thus,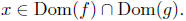 'Nuff said. Exercise 4.3.

4.4. Yes. The domain of F is void (empty).

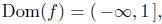and ,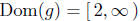

Thus,

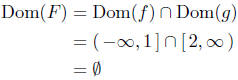
The "function" F has no domain, hence, F remains undefined.
Exercise 4.4.

4.5. This is a simple generalization of the sum/difference of two
functions.

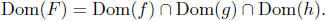
How do you calculate the values of F?

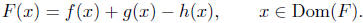
Exercise 4.5.

4.6. At the first level f can be broken down into two pieces.

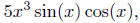and

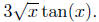
At a second level:

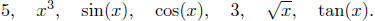
Each (much simpler) functions are the ones used to "build" the functions
f - through a combination of scalar multiplication, addition,
subtraction and multiplication of functions. Exercise 4.6.

4.7. define f(x) = 2x³ - 1, and g(x) = sin(x), then F = f⁵, and
G = g².Exercise 4.7.

4.8. Three! But is it the three you had in mind? define f(x) = x,
g(x) = sin(x), and h(x) = 1. Then,

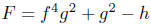
or,

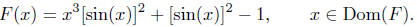
What is the natural domain of definition of F? Is there another way
of writing F?Exercise 4.8.

4.9. We say that f < g over the set A provided



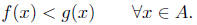
Geometrically, this means that the graph of f is always below the
graph of g when plotting these functions over the set A.

To be true to our mathematical roots we should realize what about
the set A?

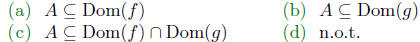
Part of successfully answering this question is being able to read and
understand the proposed questions. Then after some thought, respond
correctly with error. How did you do? Exercise 4.9.

5.1. I'll leave the details to you. But I will tell you,

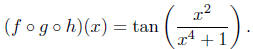
Verify! Exercise 5.1.

5.2. A challenge to our perspicacity, without doubt.

Calculation of W o M. By convention, we take as the independent
variable symbol, the symbol used by the inner-most function for its
independent variable. Thus

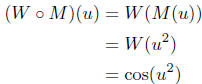
But, of course, the independent variable is a dummy, so it really didn't
matter what letter we used. Thus,

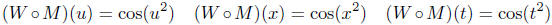
all define exactly the same function. The use of u was just a little
more convenient to use than the other variables.

Calculation of M o W. By convention, we take as the independent
variable symbol, the symbol used by the inner-most function for its
independent variable. Thus

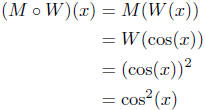
Ditto the comments made above. Exercise 5.2.

5.3. The height of triviality: I hope you got it.
Exercise 5.3.

5.4. Let 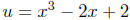, then
y = tan(u), where .
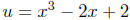Exercise 5.4.

7.1. This is a polynomial in t of degree 5 with rational coefficients.
Exercise 7.1.

7.2. First "proof by example." This is not a proof, but it is frequently
used to get insight into how to formally prove an assertion. Take as
an example:

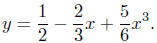
Get a common denominator for the coefficients - that would be 6.
Thus,

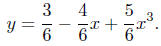
Now, factor out 1/6.

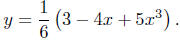
As you can see, the original polynomial is written as a rational scalar
multiple (that is, a scalar multiple that is a rational number) times a
polynomial with integer coefficients.

The general proof is an abstract manifestation of this example.
Exercise 7.2.