Probability theory is a mathematical discipline , and it is
only natural that it has been developed in
terms of the specialized notation and techniques of mathematics. The important
thing to keep in
mind is that all of the rebarbative symbolism can be translated back into the
basic language that
philosophers are more familiar with, though often the translation takes a great
deal more space
than the original statement and sometimes, if the notation is well chosen, the
translation will
obscure some important features that are brought out strikingly in the
abbreviated form.
The following notes are designed to help philosophers as
they are reading probability theory. I
have tried to presuppose only a rusty recollection of highschool math.
* fractions
* Multiplying fractions is thrillingly simple: a/b × c/d = ac/bd. This equality
can be
exploited in both directions. In probability, for example, we will sometimes
write:
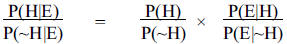
This equation separates out two ratios on the right-hand
side, which are called the prior
odds and the likelihood ratio , respectively. We arrive at it by taking the
simple form of
Bayes’s Theorem for P(H|E) and P(~H|E):
P(H|E) = P(H)P(E|H) ÷ P(E)
P(~H|E) = P(~H)P(E|~H) ÷ P(E)
We then divide P (H|E) by P(~H|E) and also do the
corresponding division on the right.
The term P(E) cancels out, leaving us with
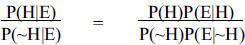
In the final step, we separate out the respective ratios
on the right-hand side.
* Adding fractions requires that we find a common
denominator. Note that in general
a/b + c/d …≠ ac/bd,
a common error known as “freshman addition.” The correct
form is
a/b + c/d = (ad + bc)/bd.
Nevertheless, for some cases of combining evidence we may
make use of something like
freshman addition.
* Sometimes we need to transpose terms in fractions.
Provided that we are careful not to
divide by zero, we may find the following transformations handy:
a/b = c <=> a/c = b (multiplying both sides by b/c)
a/b = c/d <=> d/b = c/a (multiplying both sides by d/a)
In any event, again remembering that we must restrict
ourselves to cases where there is no
division by zero, the following identity is important and worth remembering:
a/b = c/d
 <=>ad = bc (multiplying both sides by bd)
<=>ad = bc (multiplying both sides by bd)
* Comparing fractions can be tricky. Although 1/2 and 5/10
have the same value, they are
distinct fractions. In some contexts we will not want to reduce the latter to
the former. For
example, if we are flipping a thumbtack to see how frequently it lands point up,
we might
want to represent the number of successes s in a number of trials t by the
fraction s/t. If
we have flipped it twice and it has landed heads up once, then s/t will be 1/2.
Flipping it a
third time with another point-up result, we will update this to (s+1)/(t+1),
which is 2/3.
On the other hand, if we have flipped it ten times with a point -up result five
times, the
ratio s/t will be 5/10; and if we have a success on the next trial, the new
number
(s+1)/(t+1) will be 6/11, which is not equal to 2/3. Context will help us to
determine
whether it is appropriate to reduce fractions or not.
* intervals
* Quite frequently it is useful to set boundaries within
which a given variable must lie.
Probabilities, for example, may be as low as 0 or as high as 1, but they may not
exceed
these bounds. There are several useful notations that help us to indicate this.
We might
write the foregoing fact about probabilities in either of these ways:
r ∈[0, 1]
0 ≤ r ≤1
The first expression says that r is an element of the
interval [0, 1], the set of values in the
number line from 0 to 1, including the end points as possible values. The second
says that
r is a number greater than or equal to 0 and less than or equal to 1. Obviously,
these come
to the same thing.
It is a natural question why we use the weak inequalities
(≤) here rather than the strong
ones (<). The answer is that we can use the strong ones when we don’t want to
include
the endpoints. If both zero and 1 are (in some particular case) inadmissible
values, we
will write:
r ∈(0, 1)
0 < r < 1
The use of the rounded parentheses rather than the
squared-off brackets is a convention
that indicates the end points are not included; this is called an open interval,
while the
interval with endpoints included, written with square brackets , is called
closed. If for
some reason we wanted to include one endpoint but not the other, we could write
r ∈[0, 1)
or
r ∈(0, 1]
These are called half-open intervals. One useful thing to
note about half-open intervals is
that we can use them to tile the real number line without missing a single
point, e.g.
[0, 1), [1, 2), ... [n, n+1), ...
In general, we can do the same thing with real numbers a
and b instead of 0 and 1,
writing, for example, [a, b], provided that a ≤ b. In the limiting case where
the two
numbers are the same, the interval reduces to [a, a], in which case we identify
the interval
with the real number a (or, if we are being picky about it, with {a}, the set
containing a as
its only member).
* Intervals provide us with the means of indicating some
important sets that have infinitely
many members without having to use ellipses . We cannot enumerate all of the
natural
numbers, though we can start the enumeration and use a notation that indicates
how we
intend it to go on by writing {0, 1, 2, ... , n, n+1, ...}. But when it comes to
the points in a
line segment, we cannot even start the enumeration. Start with zero – what is
the very
next point? The question is misleading: there is no next point. Still, with the
compact
notation [0, 6] we can indicate precisely which set of points we have in mind,
even
though they defy an orderly enumeration.



