Question: Why is Algebra important? How can Algebra
be applied to ‘real life?’ When will I ever
use Algebra in Real Life?
Findings: See ideas below
Observations/Questions: I had endless questions about connecting Algebra
to real life. The most
important question was how I could apply this new information to teaching in my
classroom.
After doing the batting average activity, students learn how to find game
batting averages,
but it left me wondering how seasonal batting averages are found.
I also wonder how I can use more real-life Algebraic applications that relate to
sports.
I noticed that there are an endless supply of how Algebra is connected with real
life. Many
of the lessons got a bit complicated, but there are plenty of accessible ideas
for middle school.
Why did I pick this question? I picked this question because I believe it
is a crucial part of
teaching Algebra. In brain research, it has been shown that students remember
concepts much
more effectively if they have something to attach it to in their memory. By
finding real world
connections to Algebra, students will be able to find more meaning in what
they’re learning.
FINDINGS
Quadratics
Windsail Design
Activity:
Find the equations
that match the
parabolic curves being
considered in building
windsail masts.
Given three
points, determine the
quadratic function .
Investigate how
a family of curves can
be produced by |
 |
changing one parameter in the equation.
Relate changes in coefficients of a quadratic
function to their influence on the shape and position
of the parabola on the graph .
Use y = ax(x-h) h = height of mast
Resource – Futures Channel Video “Windsails”
Quadratics
Building Telescope Mirrors

Activity:
Find an equation for a new telescope mirror
with a given light-gathering power and focal length.
Graph a quadratic function, then relate the
coefficients of a quadratic function to their influence on
the shape and position of the parabola on the graph.
Use this equation for the parabola:
(y – 0) = .03125(x – 2.12)² - simplifies to :
Y - .03125x² - 0.1325x = .14045
Vertex = (2.12, 0)
Resources – Futures Channel “Looking Into Time”
EQUATIONS
Batting Averages

Activity: Find the batting averages of several
baseball players.
Solve an expression by substituting values for
variables .
If a batter has a seasonal batting average of
“S” after a total of “T” times at bat and gets “K” hits
in the game for “N” times at bat, his new batting
average is determined by this expression .
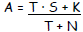
**This leaves the question “How do they get the
seasonal average in the first place?
Resource: The Futures Channel – “Ballpark”
Exponential Equations
Population Growth
 |
|
Activity:
Determine if the
populations of several
endangered species are
flourishing.
Look at the |
relationship between the “number of young produced”
(Y) and “time” (t) to model an exponential function
based on population data for several endangered
species. Compare this data with data representing
actual populations.
Use the equation Y = A · 10kt
Resource: The Futures Channel – “The Black Footed Ferret”
LINEAR EQUATIONS
Bungee Barbie

Activity: Record data to determine how many rubber
bands will adequately help Barbie to Bungee Jump
safely.
Create a scatterplot and create a line of best
fit.
Predict how many rubber bands will be needed
for Barbie to safely jump from a given height.
Algebra in the Real World
 Laura Thompson-Beato
Laura Thompson-Beato
How I would use these ideas in my classroom?
“What does Algebra have to do with the Real World?”
The connections to the ‘real world’ that I found for Algebra lend themselves
perfectly for use in the
classroom . The six ideas I talked about are using Algebra for batting averages,
finding curvatures for telescope
mirrors, designing windsail sails, studying exponential population growth, using
polynomials as applied to the shapes
of roller coasters, and using a Barbie doll to graph a bungee experiment.
The “Batting Average” lesson on The Futures Channel
includes the following information for a lesson about
45 minutes long:
If a batter goes into a game with a seasonal batting average of S after a total
of T times at bat, and gets K
hits in that game for N times at bat, his new batting average is determined by
this equation:
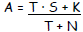
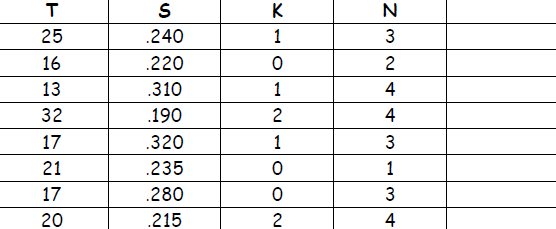
1.
| Batter |
 |
| Jackie |
| Willie |
| Roger |
| Mickey |
| Ila |
| Alta |
| Carita |
| Irma |
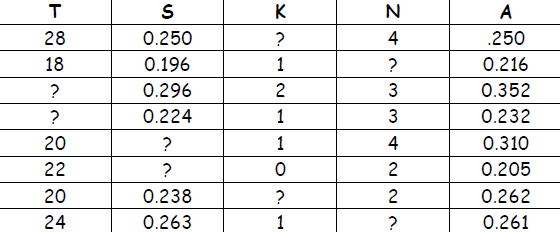
2. Find the missing number for each batter.
| Batter |
 |
| Jackie |
| Willie |
| Roger |
| Mickey |
| Ila |
| Alta |
| Carita |
| Irma |



