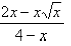Properties
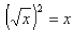for all non- negative numbers x
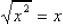for all non-negative numbers x
However , if x happens to be negative, then squaring
it will produce a positive number, which will have a
positive square root , so
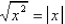for all real numbers x
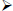You don’t need the absolute value sign if you
already know that x is positive. For example,
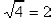, and saying anything about the absolute
value of 2 would be superfluous. You only need
the absolute value signs when you are taking the
square root of a square of a variable , which may
be positive or negative.
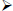The square root of a negative number is
undefined, because anything times itself will
give a positive (or zero) result.
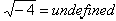(your calculator will probably
say ERROR).
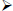Note: Zero has only one square root (itself). Zero
is considered neither positive nor negative.
WARNING: Do not attempt to do something like
the distributive law with radicals :
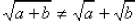(WRONG) or
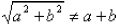(WRONG).
This is a violation of the order of operations . The
radical operates on the result of everything inside of
it, not individual terms . Try it with numbers to see:
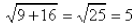(CORRECT)
But if we (incorrectly) do the square roots first, we
get
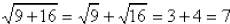(WRONG)
However, radicals do distribute over products :
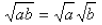
and
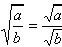
provided that both a and b are non-negative
(otherwise you would have the square root of a
negative number).
Perfect Squares
Some numbers are perfect squares, that is, their
square roots are integers:
0, 1, 4, 9, 16, 25, 36, etc.
It turns out that all other whole numbers have
irrational square roots:
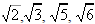, etc. are all irrational numbers.
The square root of an integer is either perfect or
irrational
C. Simplifying Radical Expressions
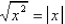for all real numbers
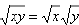if both x and y are non-negative, and
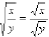if both x and y are non-negative, and y is
not
zero
WARNING: Never cancel something inside a
radical with something outside of it:
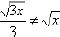WRONG! If you did this you would be
canceling a 3 with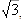 
, and they are certainly not the
same number.
The general plan for reducing the radicand is to
remove any perfect powers. We are only considering
square roots here, so what we are looking for is any
factor that is a perfect square. In the following
examples we will assume that x is positive.
Example:
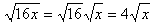
In this case the 16 was recognized as a perfect square
and removed from the radical, causing it to become
its square root, 4.
Example:
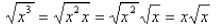
Although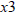 
is not a perfect square, it has a factor of
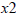, which is the square of x.
Example:
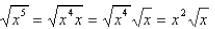
Here the perfect square factor is
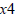, which is the
square of .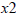
Example:
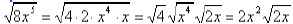
In this example we could take out a 4 and a factor of
, leaving behind a 2 and one factor of x.
The basic idea is to factor out anything that is
“square-rootable” and then go ahead and square
root it.
D. Rationalizing the Denominator
One of the “rules” for simplifying radicals is that you
should never leave a radical in the denominator of a
fraction. The reason for this rule is unclear (it
appears to be a holdover from the days of slide
rules), but it is nevertheless a rule that you will be
expected to know in future math classes. The way to
get rid of a square root is to multiply it by itself,
which of course will give you whatever it was the
square root of. To keep things legal, you must do to
the numerator whatever you do to the denominator,
and so we have the rule:
If the Denominator is Just a Single Radical
Multiply the numerator and denominator by the
denominator
Example:
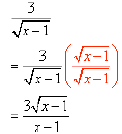
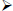Note: If you are dealing with an nth root instead
of a square root, then you need n factors of that
root in order to make it go away. For instance, if
it is a cube root (n = 3), then you need to
multiply by two more factors of that root to give
a total of three factors.
If the Denominator Contains Two Terms
If the denominator contains a square root plus some
other terms, a special trick does the job. It makes use
of the difference of two squares formula:
(a + b)(a – b) = a2 – b2
Suppose that your denominator looked like a + b,
where b was a square root and a represents all the
other terms. If you multiply it by a – b, then you will
end up with the square of your square root, which
means no more square roots. It is called the
conjugate when you replace the plus with a minus (or
vice-versa). An example would help.
Example:
Given:
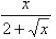
Multiply numerator and denominator by the
conjugate of the denominator:
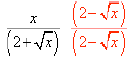
Multiply out:
