Combining Functions

♦ Perform arithmetic operations on functions
♦Perform composition of functions

Five Ways of Combining Two Functions f and g

• Addition
• Subtraction
• Multiplication
• Division
•Composition

Definitions

If f(x) and g(x) both exist, the sum , difference, product, quotient and composition of two functions f and g are defined by

•Addition
• Subtraction
• Multiplication
• Division
•Composition

Examples of Evaluating Combinations of Functions –Using Symbolic Representations

Example of Addition of Functions :

Let f(x) = x^2 + 2xand g(x) = 3x-1

Find the symbolic representation for the function f + g and use this to evaluate (f + g)(2)

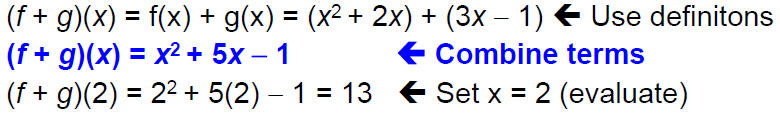
or Evaluate each function, then combine

Graphical Example of Addition of Functions

Example of Multiplication of Functions :

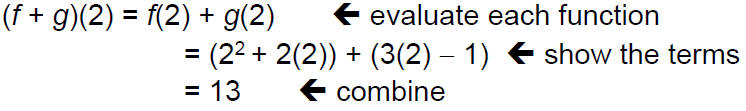
Let f(x) = x^2 + 2xand g(x) = 3x−1

Find the symbolic representation for the function fg and use this to evaluate (fg)(2)

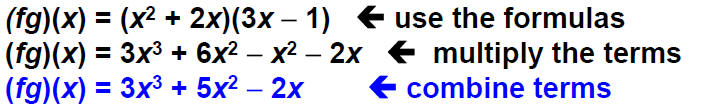
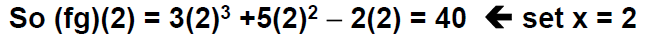
Or

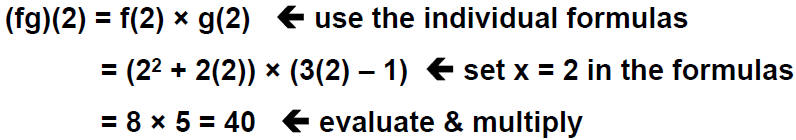
Example of Composition of Functions:

Let f(x) = x^2 + 2xand g(x) = 3x-1

Find the symbolic representation for the function 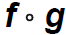and use this to evaluate (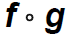)(2)

Example of Composition of Functions:

Let f(x) = x^2 + 2xand g(x) = 3x-1

Find the symbolic representation for the function 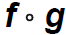and use this to evaluate (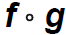)(2)

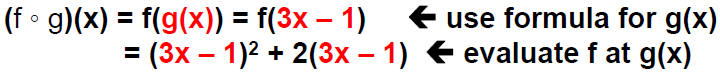
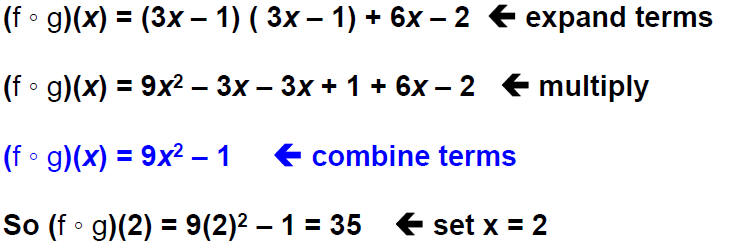
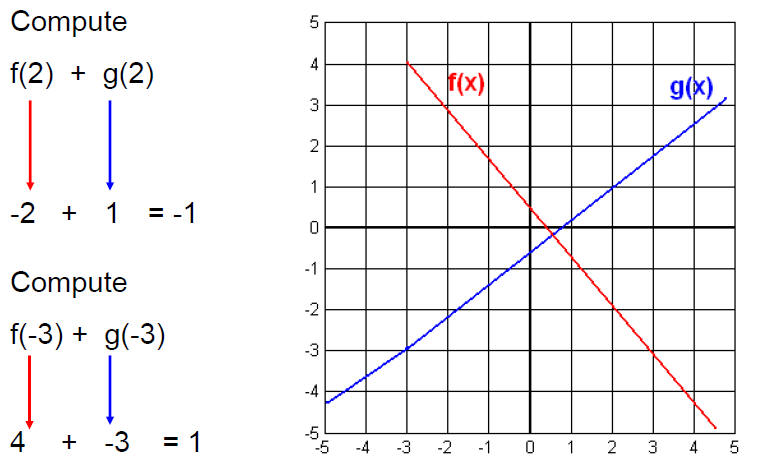
Example:

Let f(x) = 1-5x and

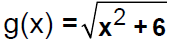
Find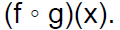

Find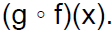

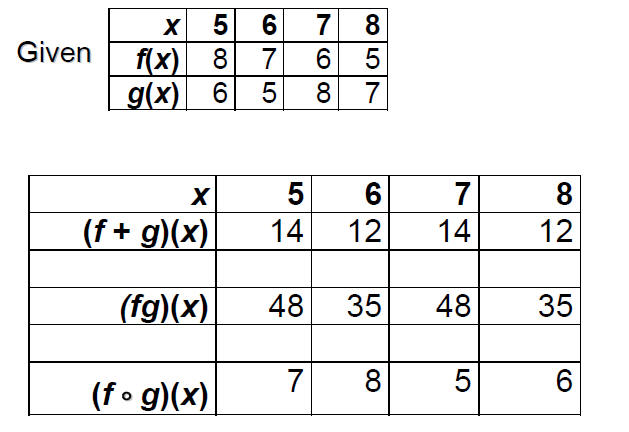
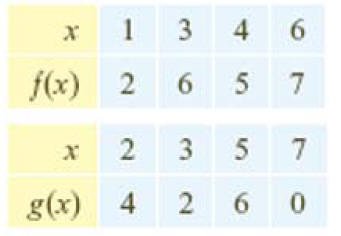
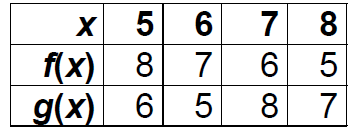
Example: Composition from tabular displays for functions.

Find (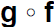)(1)
Find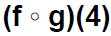
Find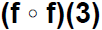

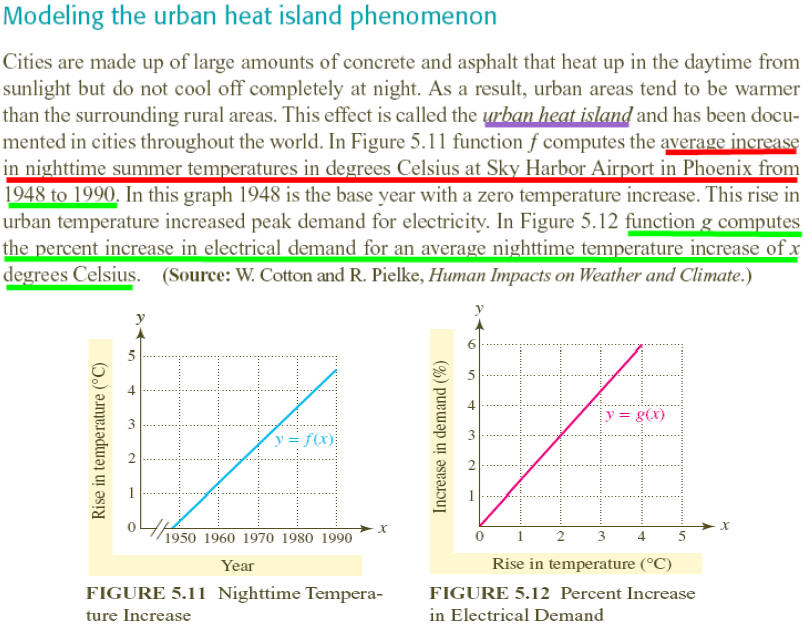
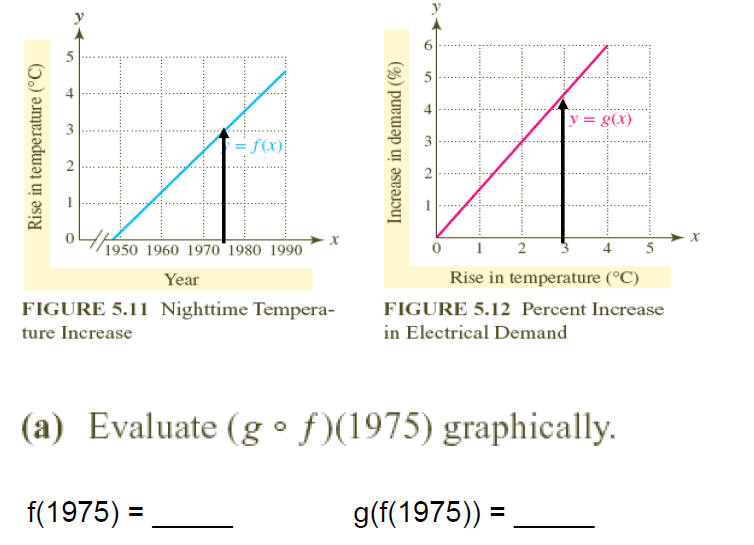
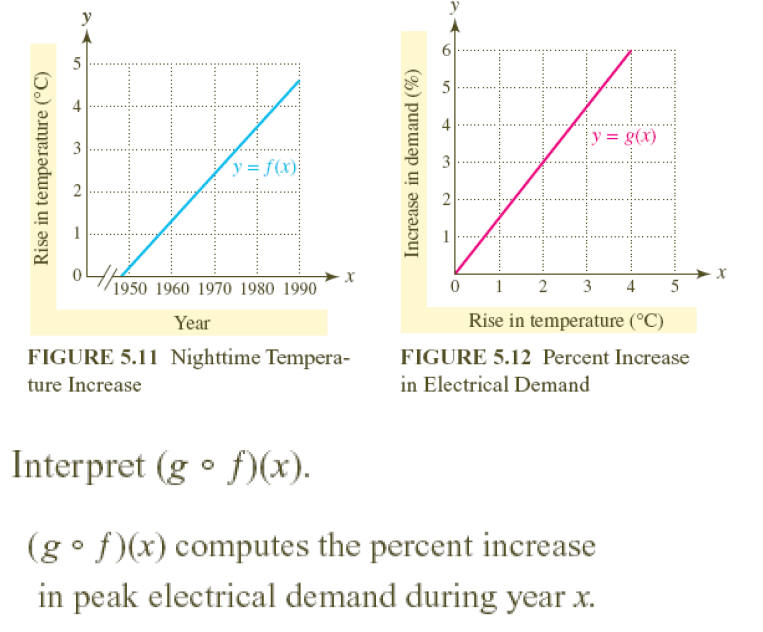
Evaluating Combinations of
Functions Numerically

•Given numerical representations for f and and g in the table

•Evaluate combinations of f and and g as specified.

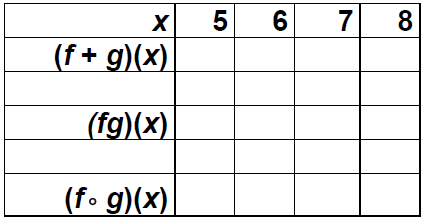
Examples:

Answers: