Leonard Pisano (i.e. Leonardo of Pisa) (1170 -1240) a.k.a. Fibonacci (i.e.
son of Bonacci)
was the greatest mathematician of the Middle Age. Being unaware of this fact (or
rather
unable to make a living on it), he worked as a merchant and diplomat and
traveled a lot.
During his traves he used to think about various mathematical problems . The
following
one from his Liber Abaci made him famous
Rabbit Problem
Suppose a newly-born pair of rabbits, one male, one female,
are put in a field. Rabbits are
sexually mature after one month so that at the end of its second month a female
can
produce another pair of rabbits. Suppose that our rabbits never die and that the
female
always produces one pair (one male, one female) every month from the second
month on.
How many pairs will there be in one year?
The nth Fibonacci number fn is the number of pairs of rabbits at
the end of the nth month.
Therefore f0 = 1, f1 = 1, f2 = 2, . . .
1 Exercise. Find f3, f4,
f5, . . . , f10. Show that:
and solve the Rabbit Problem.
Equation ?? is convenient for finding values of f n
only for small n. To find f200 for
example, we will need to perform 198 additions , and for f1000…
The goal of this project is to find a direct formula for computing fn
for arbitrary n. A
surprising thing is that in doing this we will be using power series .
Consider the power series
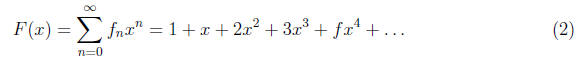
The idea is to try to find an analytic expression for the
function F(x) and then to compute
the coefficients at xn in the power series ??.
2 Exercise. Compute the ratio fn+1/fn
for the first 10 values of n. What predictions
can you make about the behavior of this ratio as
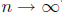? What does it tell us about the
interval of convergence of the series ???
3 Exercise. Using Equation ?? replace the
coefficient fn+2 at xn+2 in the series F(x).
Then rearrange the terms to present F (x) as the sum of two series , one related
to xF(x)
and another related to x2F(x).
Using this equation , find a formula for F(x). [Hint: Your
answer should give F(x) as a
rational function (i.e. a ratio of two polynomials ) with a quadratic function in
the
denominator.
4 Exercise. Find a power series expansion in terms
of xn for the function F(x) you
obtained in the previous problem. [Hint: You could use a Taylor series if you
knew how to
find all the derivatives of F(x) at x = 0. Since this cannot be done by a
straightforward
computation (try it!), we have to think of a better way. What could be better in
our case
than partial fractions ?]
5 Exercise. Write down the coefficient at xn
in the series you produced in the previous
problem. Comparing it with series ?? find a formula for the nth
Fibonacci number fn.
Check your formula against f0, f1, . . . , f10.
If it works, then it must be the formula found by the
French mathematician Binet in 1843.
Is not it a remarkable formula? Put the formula in a prominent place in your
report.
6 Exercise. Using your (and Binet’s) formula (and a
calculator) compute accurately
writing down the results of the intermediate calculations. Do you see that one
of the two
terms with nth powers is always very small?
7 Exercise. Using your observations from the previous
step , find a simpler procedure
for computing fn. Use it to find f40 and f50. About how
big is f100? f1000?
8 Exercise. Find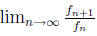
and the
interval of convergence of the series ??.
