Exponential and Logarithmic Functions

The two homework assignments for 1.6 due Wednesday by 5pm. All homework from last week due
today by 5 pm.

Graph ln (x). Compare to e ^x.

Now let's do a few properties. The following works for any base b > 0, b ≠ 1, but i'm just going to
write it down for base e. So, if a > 0 and c > 0 and r is any real number ,

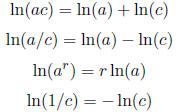
Notice that in the first two, you are multiplying (or dividing) the stu inside. In other words, DO
NOT ADD WHAT 'S INSIDE!!!!

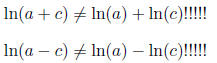
For example, ln(6) = ln(2*3) = ln(2) + ln(3). Don't tell me that ln(6) = ln(3 + 3) = ln(3) + ln(3)
because this will anger the math gods , something i advise you not to do right before (or worse,
during!) a test!!

Where do these properties come from? Remember how 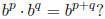We started with multiplying
the bases and we ended up adding the exponents. Now, think backwards (we are, after all,
working with the inverse of the exponential function !), and the first property falls right out. Same
thing with the others.

All right, let's do an example using all these log properties . The following two examples are
something very typical that you can see on your exam:

Example: expand out the logarithm in terms of sums, differences, and multiples of simpler
logarithms:

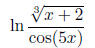
Notice we're dividing two things inside the logarithm here, the 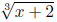and the cos(5x). So,
division inside means subtraction outside, and we now have

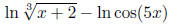
Can we do anything else? We surely can! 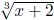is the same thing as 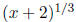, so now we get

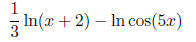
And that's pretty much it. There are no other properties we can really apply. So, let's go on to
the next example, which is the same thing only backwards.

Example: simplify the following:

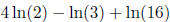
The 4ln(2) turns into ln(2⁴) = ln(16).

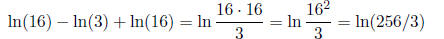
Basically, if you are adding and subtracting a whole slew of log functions, just look for the ones
you're adding, and those will be in the numerator, while the stuff inside the log functions you're
subtracting will end up in the denominator .

Let's try one with an x in it:

Example: simplify

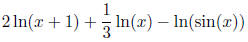
Again, first thing to do is turn all those coefficients into exponents :

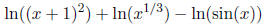
So, we get

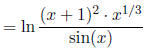
and there's not much else we can do about that...

One thing i should mention is 2 ln(x) = ln(x²), NOT (ln(x))²! The x is squared, not the log
function!

Let us go on to solving an equation when logs are present. The idea behind this is to get
everything with a log in front of it on one side, and everything else on the other. Combine all the
logs into one giant log using those properties we just practiced and then take the exponential of
both sides.

Example:
Solve for x.

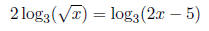
Start combining!

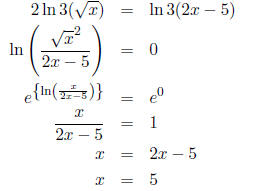
Let's do one more.
Example:

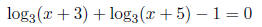
Same deal as before...only thing is now we have to set this equal to 1 instead of 0.

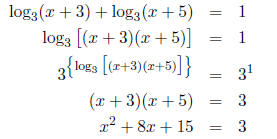
And now it's just a regular ol' quadratic, which I hope you can solve! x^2 + 8x + 12 = 0. This
means x = -6, x = -2.

Are we done? Nope. Because if we were to plug in x = -6, that wouldn't work in that rst log
function! Can't have a negative inside a log (just like you can 't have a negative under the square
root ...works the same way!). That means x = -2 is our answer. You gotta make sure you check
your answers! Sometimes they don't work!

This now brings us to how to solve for x when it's in an exponential function. Well, as mentioned
many times, the log function is the inverse, so that means if y > 0, then

y = e^x is equivalent to x = ln(y):

(again, this works for any base b, but i was just too lazy to put the others in.)

Example: Solve 2e^3x = 7.

Start o by taking ln of both sides

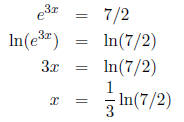
Sometimes, you can get hidden quadratics (yay!)

Example: solve for x

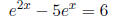
Let 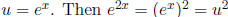, and we have

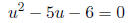
which conveniently factors nicely into (u + 1)(u - 6), and we have u = -1 or u = 6. ie, e^x = -1 or
e^x = 6. Can e^x = -1? Nope! It's never negative! Throw that answer out! This means we only
have e^x = 6, or x = ln(6).