Case 1: Fractions with like denominators .
(1) Add or subtract the numerator and place the answer over the common
denominator.
(2) Write the answer in lowest terms .
Example1:
a) Add: 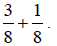
b) Subtract: 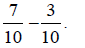
Solution : a) Since the denominators are the same, add the
numerators and keep the
denominator the same.
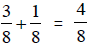
Since 4/8 is not in lowest terms , divide numerator and
denominator by 4 to get 1/2.
b) Again the denominators are the same, so we just
subtract the numerators and
place that answer over the common denominator .
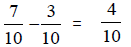
Since 4/10 is not in lowest terms, divide numerator and
denominator by 2 to get 2/5 .
Case 2: Fractions with unlike denominators.
(1) Find equivalent fractions for each original fraction,
so that both fractions have a common
denominator.
(2) Follow the procedure for like denominators .
Example 1:
Add: 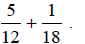
Solution: Since we have unlike denominators, we
need to determine a common denominator
between 12 and 18. To do this, we need to look at the multiples of 12 and 18 and
find the
smallest common multiple.
Multiples of 12 are: 12, 24, 36, 48, …
Multiples of 18 are: 18, 36, 54, 72, …
Since 36 is the 1st multiple in common, that will be our common denominator.
(You could also just multiply their denominators together to find a common
multiple but this often
leads to large numbers which are not easily simplified.)
Next , we need to write equivalent fractions for each of our original fractions,
having a
common denominator of 36.
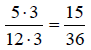 Since 12 ⋅ 3 = 36, we
multiply numerator and denominator by 3.
Since 12 ⋅ 3 = 36, we
multiply numerator and denominator by 3.
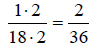 Since 18 ⋅ 2 = 36, we
multiply numerator and denominator by 2.
Since 18 ⋅ 2 = 36, we
multiply numerator and denominator by 2.
Now that we have common denominators, we can add the
numerators and place that over
the common denominator,
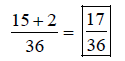
Example 2:
Subtract: 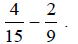
Solution:
Multiples of 15 are: 15, 30, 45, 60,…
Multiples of 9 are: 9, 18, 27, 36, 45,…
Since 45 is the 1st multiple in common, that will be our common denominator.
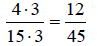 Multiply numerator and
denominator by 3.
Multiply numerator and
denominator by 3.
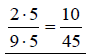 Multiply numerator and
denominator by 5.
Multiply numerator and
denominator by 5.
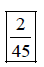 Subtract numerators and
place answer over common denominator.
Subtract numerators and
place answer over common denominator.
**********************************************************************************************************************************
**
Now You Try (Section 6)
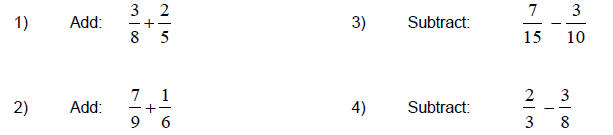
(Answers to Now You Try (Section 6) are found on page 30.)
**********************************************************************************************************************************
**
Section 7: Multiplying Fractions
To Multiply Fractions
(1) Divide out any common factors between any numerator and any denominator.
(2) Multiply remaining numbers in the numerator, then multiply remaining numbers
in the denominator.
(3) Place the product of the numerators over the product of the denominators.
(4) Check that the answer is in lowest terms.
Example 1:
Multiply: 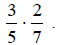
Solution: Since there are no common factors between
any of the numerators and denominators, we
simply multiply the numerators, then multiply denominators.
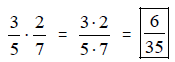 which is in lowest
terms.
which is in lowest
terms.
Example 2: Multiply:
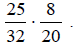
Solution: 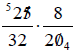 Divide 20 and 25 by their common factor of 5.
Divide 20 and 25 by their common factor of 5.
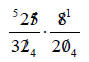 Divide 8 and 32 by
their common factor of 8.
Divide 8 and 32 by
their common factor of 8.
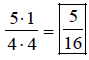 Multiply remaining
numbers in the numerator and denominator.
Multiply remaining
numbers in the numerator and denominator.
Answer is in lowest terms.
**********************************************************************************************************************************
**
Now You Try (Section 7)
Multiply:

(Answers to Now You Try (Section 7) are found on page 30.)
**********************************************************************************************************************************
**
Section 8: Dividing Fractions
Definition: If a/b is a fraction, the fraction b/a is
called the reciprocal of a/b .
To Divide Fractions
(1) Rewrite the 1st fraction as it is given.
(2) Change the division sign to a multiplication sign.
(3) Write the reciprocal of the 2nd fraction.
(4) Use the rules for multiplying fractions.
Example 1:
Divide:
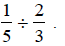
Solution: 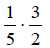 Multiply
by the reciprocal.
Multiply
by the reciprocal.
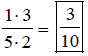 Multiply numerators,
then multiply denominators. Answer in lowest terms.
Multiply numerators,
then multiply denominators. Answer in lowest terms.
Example 2:
Divide:
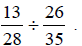
Solution:
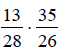 Multiply by the
reciprocal.
Multiply by the
reciprocal.
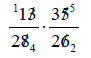 Divide out any common
factors between any numerator and any
Divide out any common
factors between any numerator and any
denominator (divide 28 and 35 by 7 ; 13 and 26 by 13).
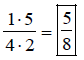 Multiply numerators,
then multiply denominators. Answer is in lowest terms.
Multiply numerators,
then multiply denominators. Answer is in lowest terms.
Example 3:
Divide: 
Solution:
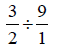 Write 9 as a fraction
by placing a 1 in the denominator.
Write 9 as a fraction
by placing a 1 in the denominator.
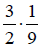 Multiply by the
reciprocal.
Multiply by the
reciprocal.
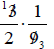 Divide 3 and 9 by 3.
Divide 3 and 9 by 3.
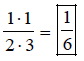 Multiply numerators,
then multiply denominators. Answer is in lowest terms.
Multiply numerators,
then multiply denominators. Answer is in lowest terms.
**********************************************************************************************************************************
**
Now You Try (Section 8)
Divide:
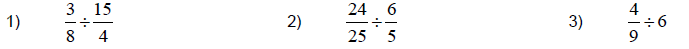
(Answers to Now You Try (Section 8) are found on page 30.)
**********************************************************************************************************************************
**
Section 9: Mixed Numbers
A number of the form 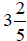 is called a mixed number because it is composed of a whole number and a
fraction.
is called a mixed number because it is composed of a whole number and a
fraction.
Sometimes people misinterpret it to mean 3 times 2/5. In general, a number of
the form 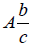 means
means
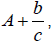
so 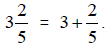 Mixed numbers are helpful to get a better
idea of the size of a number. For example, when you
Mixed numbers are helpful to get a better
idea of the size of a number. For example, when you
look at an improper fraction such as 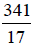 it is
difficult to get a feeling for its size. However, if we write
it is
difficult to get a feeling for its size. However, if we write
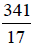 as the
as the
mixed number, 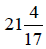 , we have a better feeling for
its size.
, we have a better feeling for
its size.
To Change from an Improper Fraction to a Mixed Number
(1) Divide the denominator into the numerator. This quotient becomes the whole
number part of the mixed
number.
(2) If the denominator does not divide evenly into the numerator, place the
remainder over the denominator.
This becomes the fractional part of the mixed number.
Example 1:
Change 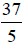 to a mixed
number.
to a mixed
number.
Solution:
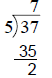 Divide the denominator
into the numerator. Since 2 is the remainder, place that over the denominator 5.
Divide the denominator
into the numerator. Since 2 is the remainder, place that over the denominator 5.
Write as a mixed number.
Therefore, 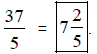
To Change from a Mixed Number to an Improper Fraction
(1) Multiply the whole number and the denominator, add the result to the
numerator.
(2) Place the answer from step (1) over the denominator.
Example 1:
Change 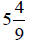 to an improper
fraction.
to an improper
fraction.
Solution:
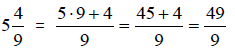
Therefore, 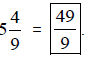
**********************************************************************************************************************************
**
Now You Try (Section 9.1)
1) Change the following improper fractions to mixed
numbers.

2) Change the following mixed numbers to improper
fractions.

(Answers to Now You Try (Section 9.1) are found on page
30.)
**********************************************************************************************************************************
**
Adding and Subtracting Mixed Numbers
Case 1:
(1) Leave the mixed numbers as mixed numbers.
(2) Find a common denominator and write equivalent fractions for the fractional
parts.
(3) Add or subtract the fractional parts. When subtracting, you may need to
borrow. (See
example below.)
(4) Add or subtract the whole number parts.
(5) Write the fractional part in lowest terms.
Example 1:
Add: 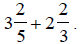
Solution:
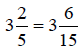 Find a common
denominator of 15.
Find a common
denominator of 15.
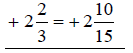 Write equivalent
fractions.
Write equivalent
fractions.
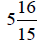 Add the whole numbers,
then add the fractions.
Add the whole numbers,
then add the fractions.
Since 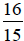 is improper, we
need to change it to a mixed number
is improper, we
need to change it to a mixed number 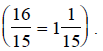
Now we can add 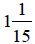 to 5,
giving us
to 5,
giving us 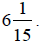
Therefore, 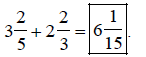
Example 2:
Subtract:
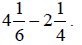
Solution:
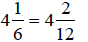 Find a common
denominator of 12.
Find a common
denominator of 12.
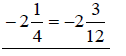 Write equivalent
fractions.
Write equivalent
fractions.
Since we cannot subtract
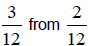 we need to borrow 1 from the 4, making it a
3.
we need to borrow 1 from the 4, making it a
3.
Since we have 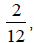 we need to write 1 as an
equivalent fraction of
we need to write 1 as an
equivalent fraction of 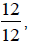 so they have a
so they have a
common denominator. The we can add 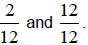
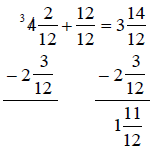 Now we can subtract.
Now we can subtract.
Therefore, 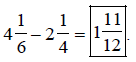
Case 2: Change the mixed numbers to improper
fractions and use the rules given for adding and
subtracting fractions. If you use this method you will not need to borrow when
subtracting.
Example 1:
Add:
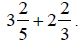
Solution:
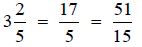 Change to improper
fractions.
Change to improper
fractions.
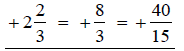 Find a common
denominator and write equivalent fractions.
Find a common
denominator and write equivalent fractions.
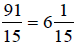 Add numerators, write
sum over the common denominator. Write answer as a mixed number.
Add numerators, write
sum over the common denominator. Write answer as a mixed number.
Therefore,
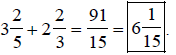
Example 2:
Subtract: 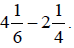
Solution:
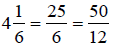 Change to improper
fractions.
Change to improper
fractions.
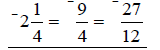 Find a common
denominator and write equivalent fractions.
Find a common
denominator and write equivalent fractions.
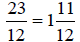 Subtract numerators,
write difference over the denominator.
Subtract numerators,
write difference over the denominator.
Write answer as a mixed number.
Therefore, 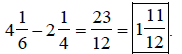
**********************************************************************************************************************************
Now You Try (Section 9.2)

(Answers to Now You Try (Section 9.2) are found on page
30. )
**********************************************************************************************************************************
Multiplying and Dividing Mixed Numbers
Change all mixed numbers to improper fractions and use the
rules given for multiplying and dividing fractions.
Example 1:
Multiply:
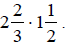
Solution:
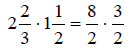 Change to improper
fractions.
Change to improper
fractions.
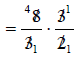 Divide out common
factors between any numerator and any denominator.
Divide out common
factors between any numerator and any denominator.
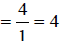 Multiply
numerators, then multiply denominators.
Multiply
numerators, then multiply denominators.
Therefore, 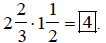
Example 2:
Divide:
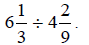
Solution:
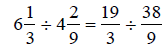 Change to improper
fractions.
Change to improper
fractions.
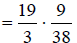 Multiply by the
reciprocal.
Multiply by the
reciprocal.
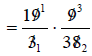 Divide out common
factors between any numerator and any denominator
Divide out common
factors between any numerator and any denominator
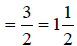 Multiply numerators,
then multiply denominators Write as a mixed number.
Multiply numerators,
then multiply denominators Write as a mixed number.
Therefore, 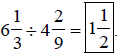
**********************************************************************************************************************************
Now You Try (Section 9.3)

(Answers to Now You Try (Section 9.3) are found on page
30. )
**********************************************************************************************************************************



