What is a proof?
Proofing as a social process, a communication art.
Theoretically, a proof of a mathematical statement is no
different than a logically valid argument starting with
some premises and ending with the statement. However,
in the real world such logically valid arguments can get so
long and involved that they lose their "punch" and require
too much time to verify.
In mathematics, the purpose of a proof is to convince
the reader of the proof that there is a logically valid
argument in the background. Both the writer and the
reader must be convinced that such an argument can be
produced – if needed.
Writing mathematical proofs is therefore an art form (the
art of convincing) and a social process since it is directed
at people (the readers).
A mathematical proof of a statement strongly depends
on who the proof is written for. Proofs for a research
audience are quite different from those found in
textbooks. And even textbook proofs look different
depending on the level of the audience (high school vs.
college vs. graduate school).
To simplify our task in this course, you will write all of
your proofs with a specific audience in mind:
ME!
That is, you are writing to convince me that you could
drop down to the logic level and provide all the details, if I
asked you to do so.
Rigor in proofs.
The above remarks should not be construed to mean that
you can get sloppy with your proofs – your audience
requires clarity, precision and, above all, correctness.
Phrases such as "clearly" or "it is easy to see that" are
neither clear nor easy for this audience.
When you say something follows from a definition, I
want to know "the definition of what?"
General Hints
The importance of definitions.
It can not be overemphasized how important definitions
are. Without a clear and crisp understanding of a
definition, you will not be able to use it in a proof. You
have to be able to recall a definition precisely when it is
needed – vague familiarity will not work for you.
Working backwards.
There is a big difference between discovering a proof
and presenting a proof. In presenting a proof you must be
convincing, and things need to follow in a logical order .
To discover a proof, you are under no such restrictions
and often the best procedure is to work the problem
backwards.
Methods of Proof
We will survey the basic proof methods. In doing so, our
examples to illustrate the techniques should not be very
complicated ... so we will restrict them to fairly simple
statements which do not need a great deal of background
to understand.
The Theory of Numbers provides an excellent source
for such examples ... so most of our examples will deal
with numbers in this section. Remember that our aim is
not to learn more about the theory of numbers, most of
the examples will be statements that you know are true,
rather we are interested in the way that the proofs are
constructed... so, concentrate on the techniques.
Direct Proof
In a direct proof one starts with the premise
(hypothesis) and
proceed directly to the conclusion with a chain of implications.
Most simple proofs are of this kind. |
Definitions:
An integer n is odd iff there exists an integer k so that n = 2k+1.
An integer n is even iff there exists an integer k so that n = 2k.
Example of a direct proof:
If n is an odd integer then n2 is odd.
Pf: Let n be an odd integer.
There exists an integer k so that n = 2k+1.
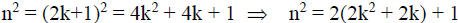
Since 2k2 + 2k is an integer, n2 is odd.
Contrapositive Proof
When proving a conditional, one can prove the
contrapositive
statement instead of the original – this is called a contrapositive
proof. |
Example:
If n2 is an odd integer, then n is odd.
Pf: Suppose n is an even integer.
There exists an integer k so that n = 2k.
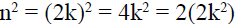
Since 2k2 is an integer, n2 is even.
Contradiction Proofs
This proof method is based on the Law of the Excluded Middle.
Essentially, if you can show that a statement can not be false, then
it must be true. In practice, you assume that the statement you are
trying to prove is false and then show that this leads to a
contradiction (any contradiction).
This method can be applied to any type of statement, not just
conditional statements.
There is no way to predict what the contradiction will be.
The method is wide-spread and is often found in short segments
of larger proofs. For example, ...
Another Contrapositive Proof
Definition: An integer n divides an integer m, written n|m, iff there exists an
integer k so that m = nk.
Example:
If A and B are integers and B ≠ 0. Show that if A
divides B then |A| ≤ |B|.
Pf: Suppose that |A| > |B|. (Note that A ≠ 0.)
Then 1 > |B|/|A| > 0.
If A | B then there is an integer k so that B = Ak.
k = B/A and the integer |k| = |B|/|A|.
But, there is no integer 1 > |k| > 0.
So A does not divide B.
Contradiction Proof
Definition: A real number r is rational iff it can be
written as r = a/b with a
and b integers and b ≠ 0. A real number is irrational if it is not rational.
Example:
The 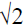 is irrational.
is irrational.
Pf: BWOC assume that 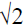 is rational .
is rational .
There exist integers p and q so that 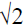 = p/q.
= p/q.
We may assume that the fraction is reduced ,
i.e. no integer divides both p and q.
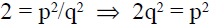 , so p2 is even.
, so p2 is even.
Thus, p is even.
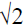 is irrational
is irrational
There exists an integer k so that p = 2k.
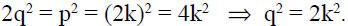
So, q2 is even and therefore q is even.
Since 2 divides both p and q we have a contradiction
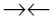
So, 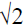 is not rational.
is not rational.
This proof is due to Euclid, but the theorem dates back to
Pythagoras and the Pythagoreans.
Proofs of Biconditionals
proof of a  statement usually uses the
tautology statement usually uses the
tautology
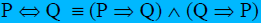
That is, we prove an iff statement by seperately proving the "if" part
and the "only if" part. |
Example:
Integer a is odd if and only if a+1 is even.
Pf: (Sufficiency, if a is odd then a+1 is even)
Suppose a is an odd integer.
There exists an integer k so that a = 2k + 1.
a+1 = (2k+1) + 1 = 2k+2 = 2(k+1)
Since k+1 is an integer, a+1 is even.
Example:
Integer a is odd if and only if a+1 is even.
Pf: (Necessity, if a+1 is even then a is odd)
Suppose a+1 is an even integer.
There exists an integer k so that a+1 = 2k.
a = a + 1 – 1 = (2k) - 1 = (2(k-1) + 2) – 1 = 2(k-1) + 1
Since k-1 is an integer, a is odd.
Uniqueness Proofs
Proofs of existentially quantified statements (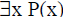 ) can be
) can be
constructive – in which case you produce an x which makes P(x)
true, or non-constructive – when you use contradiction to show
that ~(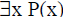 ) is false.
) is false.
Definition: To say that there is one and only one x which makes
the predicate P(x) true, we write (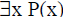 ) (there exists a unique
) (there exists a unique
x such that P(x)).
To prove a (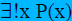 )
statement, we first prove ( )
statement, we first prove (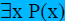 ) and then ) and then
show that if P(x) and P(y) are both true, we must have x = y. |
Definition: Let a and b be two positive integers. If n is
a positive integer and a|n
and b|n, then we call n a common multiple of a and b. If n is a common multiple
of a and b, and if for every other common multiple , m, of a and b we have that
n|m, we say that n is a least common multiple of a and b. In this case, we write
n = LCM(a,b).
Example:
For all positive integers a and b, LCM(a,b) is unique.
Pf: (We shall omit the proof of the existence of the LCM
and just show it's
uniqueness, assuming that it exists.)
Let a and b be positive integers.
Suppose m1 and m2 are two LCM's for a and b.
Since m1 is an LCM and m2 is a common multiple, m1|m2, so m1 ≤ m2.
Since m2 is an LCM and m1 is a common multiple, m2|m1, so m2≤ m1.
Therefore, m1 = m2.



