LIST OF SUGGESTED PROJECT PROBLEMS

Problem 1. Show that if the edges of the complete graph on eight vertices are
colored red and green, then there is either a three-circuit or a four-circuit whose
edges are the same color. (Wiki: complete graph, circuit ( graph theory )).

Problem 2. Use the pigeonhole principle to prove that every rational number m/n
has a decimal expansion that either terminates or repeats. In the case where a
rational number has a repeating decimal expansion, find an upper bound (in terms
of the denominator n) on the number of digits in the repeating part. (Hint: use
long division, think about possible remainders; Wiki: pigeonhole principle).

Problem 3. On the eve of an election, a radio station is forced to play 20 campaign
ads in a row. Of these 20 ads, 15 are for the Tory candidate and 5 are for the Labour
candidate. Prove that the station must play at least three Tory ads in a row at some
point. What is the minimum number of Labour ads that make possible a schedule
without 3 Tory ads in a row. (Wiki: pigeonhole principle).

Problem 4. Line 1 of the Rio de Janeiro Metro has 18 lines. How many different
way are there to divide the line into three segments, where each segment contains
at least one station? Derive the general formula for dividing a line with n stations
into k non-empty segments.

Problem 5. Prove by induction that on a n*n chessboard a knight can move from
any square to any other square via a sequence of moves for all n≥4. (Wiki: knight
(chess)).

Problem 6. Prove by induction that Lucas numbers L_n are related to Fibonacci
numbers F_n by

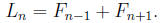
(Wiki: Lucas number, Fibonacci number).

Problem 7. Derive a bound on the Fibonacci numbers F_n of the form

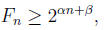
where α > 0. You have to explicitly specify numbers α and β, but your bound does
not have to be the best possible. (Wiki: Fibonacci number).

Problem 8. Suppose you are given a sequence of numbers a₁, a₂, . . . , a_k. Find a
formula for a polynomial p (x) such that p(n) = a_n for all n = 1; 2; . . . ; k.

Problem 9. Between 1970 and 1975, the National Football League was divided into
two conferences , with 13 teams in each conference. Each team played 14 games in
a season. Would it have been possible for each team to play 11 games against team
s from its own conference and 3 games against teams from the other conference?

Next two exercises deal with the method of using check digits in ISBN numbers.
Prior to 2007, every commercially available book was given a 10-digit International
Standard Book Number, usually printed on the back cover next to the barcode.
The final character of this 10-digit string is a special digit used to check for errors
in typing the ISBN number. If the first nine digits of an ISBN number are a_j ,
j = 1; . . . ; 9, the tenth digit is given by the formula

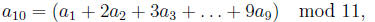
where a₁₀ = X if the answer is 10

Problem 10. Show that the check digit will always detect the error of switching
two adjacent digits. that is, show that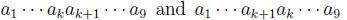
have different check digits. Show that the check digit will always detect the error of
changing a single digit.

Problem 11. Unfortunately, there were too many books and not enough ISBN
numbers. Effective January 2007, ISBN numbers must be 13 digits long. The check
digit scheme for 13-digit ISBNs is different. Explain why the obvious modification

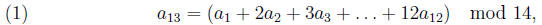
will not work. Namely, find a 12-digit string such that the quantity in equation (1)
does not change after changing a single digit. Will this modification detect the error
of switching two adjacent digits?

Problem 12. Let f : X -> Y and g : Y -> Z be functions such that 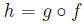is
a bijection. Prove that f is 1-to-1 (an injection) and that g is onto (a surjection).
Show that this result cannot be improved: give an example where f is not a bijection
but 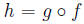is.

Problem 13. The following axioms characterize projective geometry. The undefined
terms are "point", "line", and "is on".

(1) For every pair of points x and y, there is a unique line l such that x is on l and y is on l.
(2) For every pair of lines l and m, there is a point x on both l and m.
(3) There are (at least) four distinct points, no three of which are on the same line.

Prove the following statements in projective geometry:

(1) There are no parallel lines.
(2) For every pair of lines l and m, there is exactly one point on both l and m.
(3) There are (at least) four distinct lines such that no point in on three of them.

Problem 14. The following axioms characterize Badda-Bing axiomatic system. the
undefined terms are "badda", "bing" and \hit".

(1) Every badda hits exactly four bings.
(2) Every bing is hit by exactly two baddas.
(3) If x and y are distinct baddas, each hitting bing q, then there are no other
bings hit by both x and y.
(4) There is at least one bing.

Construct a model for this system which uses the least possible number of bings
(list all baddas, bings and their relationships - which baddas hit which bings).

Problem 15. The NAND connective (symbol 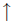) is defined by the following truth
table:

Show that p 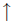q is logically equivalent to 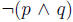. The NAND connective is
important because it is easy to build an electronic circuit (a logic gate ) that computes
NAND of two signals. Moreover, it is possible to build logic gates for other logical
connectives entirely out of NAND gates. Prove this by showing that

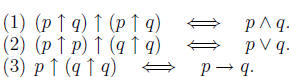
(4) Write and prove an expression for 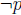in terms of p and .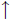

Problem 16. 1.3.d3, generalize with arbitrary q instead of 2.
Problem 17. 1.4.d7
Problem 18. 1.4.d8
Problem 19. 2.3.d1, 2.3.d2
Problem 20. 3.1.d5, find a function which is continuous at every irrational point and discontinuous at every rational point.
Problem 21. 3.2.d5, 3.3.d2
Problem 22. 4.1.d3
Problem 23. 4.1.d5
Problem 24. 5.1.d4
Problem 25. 5.1.d3