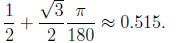Math 171 Review for the Final Exam Solutions

1. Find the limits (4 points each)

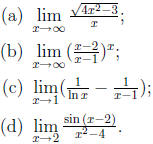
Solutions (a) The limit represents an indeterminate
form 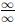. Therefore we can keep only the leading terms in the
numerator and in the denominator of the fraction .
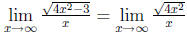. Because x tends to positive infinity we have
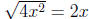whence .

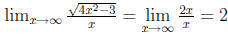(b) The limit 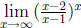represents an indeterminate form 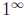. As
always when we deal with such an indeterminate form we will first
find the limit of the natural logarithm of our expression . We have
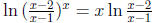, and the limit 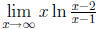is an indeterminate
form 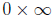because the first factor tends to ∞ and the second one -
to ln 1 = 0. To apply the L'Hospital's rule we have to write the last
limit as an indeterminate form 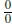or 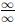. In our case it is easier to write
it in the form 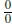, namely, 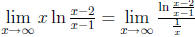. According to the
L'Hospital's rule we will now differentiate the numerator and the
denominator and look at the following limit (when differentiating the
numerator we combine the chain rule and the quotient rule).

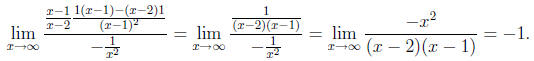
Therefore .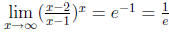

(c) We have here an indeterminate form 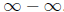. First we bring it to
the form , .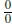

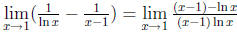Next we use the L'Hospital's rule to obtain the following limit

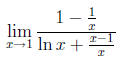
It is still an indeterminate form 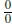so we apply the L'Hospital's rule
once again and get the limit

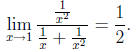
(d)

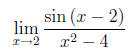
This is an indeterminate form 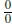and we apply the L'Hospital's rule.

2. Find the derivatives of y = f(x) with respect to x (4 points each)

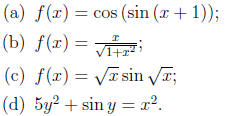
Solutions.

(a) f(x) = cos (sin (x + 1)). We apply the chain rule to get

f'(x) = -sin (sin (x + 1)) cos (x + 1):

(b)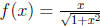 . By the quotient rule combined with the chain rule
we have

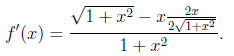
We simplify the last expression by multiplying both numerator and
denominator by .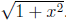

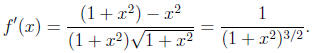
(c) 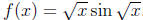. By the product rule combined with the chain
rule we have

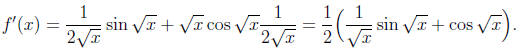
If we recall the formula

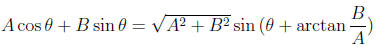
then we can also write our answer as

(d) 5y² + sin y = x². We apply implicit differentiation to get

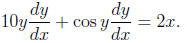
Solving it for 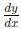we get

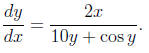
3. Find the integrals (5 points each)

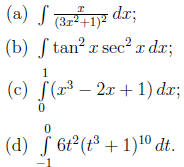
Solutions

(a)

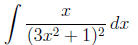
If we notice that x is proportional to the derivative of 3x² + 1 we can
use the following substitution, u = 3x² +1. Then 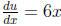, du = 6xdx,
and therefore 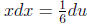. The integral becomes

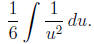
Applying the power rule we get

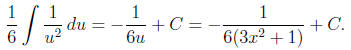
(b)

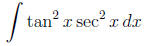
Notice that sec² x equals to the derivative of tan x and therefore it is
convenient to use the substitution u = tan x. Then du = sec² xdx and
our integral becomes

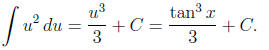
(c) We apply the power rule and the Newton - Leibnitz formula to get

(d)

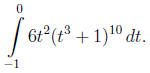
We use the substitution u = t³ + 1. Then du = 3t²dt whence
6t²dt = 2du. If t = -1 then u = 0, and if t = 0 then u = 1, we will
change the limits of integration accordingly.

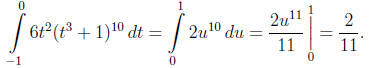
4. Use a linear approximation to estimate the following values (5 points
each)

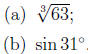
Solutions In both cases we use the formula for linear approximation

L(x) = f(a) + f'(a)(x - a)

where point a should satisfy two (informal) conditions

• a should be close to x
• the values of f (a) and f0(a) should be easy to compute.

(a) In this case we take 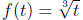whence 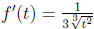. We also take
a = 64 and x = 63. Then f(a) = 4, 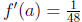, and x - a = -1. The
corresponding linear approximation to 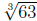is

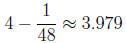
(b) Remember that we do not use the degree measure in calculus. In
our case we take

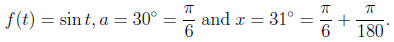
Then

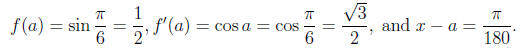
Therefore the value of the linear approximation is