Given P(x) = 5x2 −10x + 2
1. Find the zeros of P(x).
2. Find the y- intercept of P (x). Please express the
y-intercept as an ordered pair .
3. Find the vertex of P (x).
4. Using the answers you got from #1-3, graph P (x) below.
5. GivenM(x) = x3 − 2x2 − 33x +10 , is (x+5) a factor? Is (x-1) a factor?
6. Given Q(x) = x4 − 2x3 − 4x2 +11x − 6. Thanks to
Descartes’ Rule of Signs, we
can tell the number of possible positive real zeros and negative real zeros of
Q(x).
Demonstrate below (showing arrows, etc.) how we can tell.
7. How many roots are there in Q(x)?
8. Please list all the possible rational roots of Q(x).
(There should be eight of them.)
9. Testing the possible rational roots from #8, find which
ones are actually roots.
10. You found rational roots in #9. Let’s call them
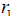and
.
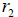We want to find the
other roots. Here’s what we can do: divide Q (x) by
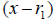to get a cubic. Then
divide the cubic by
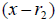to get a quadratic . Finally, use the quadratic formula
to find the last two roots of Q(x).
Show all work and be neat! ☺
In #1-5, find the zeros of each polynomial
1. P(x) = 2x2 −11x −156
2. Q(x) = 4x2 + 5x − 4
3. R(x) = x4 − 3x2 + 2x3
4. S(x) = −2x2 − 3x + 9
5. T(x) = x3 − 3x2 + 2x
6. Given the roots -2, 3, and 4, write the
polynomial of least degree .
7. Given the roots 5i, -5i, and 2, write the
polynomial of least degree.
8. Find the discriminant of
U(x) = 5x2 − 3x + 2. What does this
tell you about the roots?
9. If the discriminant of a quadratic
function is greater than zero, what do
we know about the function’s roots?
10. Find the remainder of
(x3 − 5x2 − 3) ÷ (x −1), using
synthetic division . Is (x −1) a factor?
How do you know?
11. Find the remainder of
(x3 + 4x2 − 6x +1) ÷ (x −1), using
synthetic division. Is (x −1) a factor?
How do you know?
12. Find the roots of
f (x) = −3x2 −12x + 8 by completing
the square. Plus, find the coordinates
of the vertex and the y-intercept. Then
graph it.
13. Continuing from the previous problem,
describe the transformations that have
taken place to produce f (x) from the
parent graph y = x2.
14. Find the roots of g(x) = 14 − 6x − x2
by any method. Plus, find the
coordinates of the vertex and the yintercept.
Then graph it.
15. You are given a polynomial V (x) that
has a degree of 3, and has only one
real root . Sketch a graph of what
V (x) could possibly look like .
For problems #16-20, consider
W(x) = 4x3 − 3x2 − 25x − 6 .
16. How many zeros are there?
17. How many possible positive real zeros
are there?
18. How many possible negative real
zeros are there?
19. What are the possible rational zeros?
20. Find all the zeros. (Show that you can
use the shortened form of synthetic
division.)
21. You are given a graph:
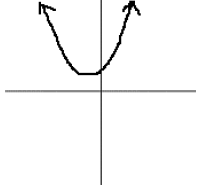
Choose which of the following two
equations could fit the graph. Explain
why you chose that equation. (Your
explanation should include something
about the nature of roots...)
a) f (x) = 2x2 + x +1
b) f (x) = 2x2 + 3x +1
22. Given use the h(x) = x4 + 2x3 − 6x − 4
location principle to find where the
approximate locations of all the real
zeros are. (Use integral steps.)
23. Given j(x) = 4x3 − 2x2 −12x +1, use
the location principle to find where the
approximate locations of all the real
zeros are. (Use steps of one -tenth.)
24. Sketch a nice graph of j(x) .
