One of the problems in describing and studying properties
of special classes of stochastic
processes is to find a convenient way of parametrizing them. The general way of
describing
stochastic processes by a consistent family of finite dimensional distributions,
satisfying
suitable additional conditions to provided regularity of sample paths is useful
only in
special cases. The finite dimensional distributions have to be provided. The
Gaussian
ones are natural and a Gaussian process can be specified by its mean and
covariance. The
only other large class is diffusion processes for which the finite dimensional
distributions
can be specified in terms of fundamental solutions of certain parabolic partial
differential
equations.
A convenient way of describing a discrete time stochastic process is through
succesive
conditional distributions, i.e.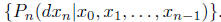 
This has the
advantage that if
the index set is really time, this decribes a model for the evolution of the
process.
The continuos time analog of this is not so obvious. In the deterministic case a
con-
tinuos evolution can be described in the simplest case by an ordinary
differential equation ,
the discrete anlog of which is a recurrence relation. If one thinks of the
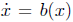
as describing a an approximate recurrence of the form
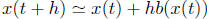, then in
the stochastic case we are looking for an approximate way of normalizing the
conditional
distribution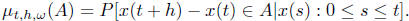 
If one thinks of the ODE
as describing a vector filed that is tangent to the curve, then one has to
define some sort
of tangent to a stochastic process. Since the tangent is a blowup of a small
difference we
need to blow up the samll distribution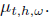
This
is done by convoluting it with itself
[ 1/h] times. Note that in the deterministic case this is essentially the same
as dividing by
h or adding it to itself [ 1/h ] times. In the limit the high convolution, if it
has a limit will
converge to an infinitely divisible distribution
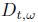which can be called the tangent.
Example 1. If x(t) is Brownian motion, then
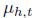is Gaussian with mean 0 and vaiance
h and the limiting tangent is the normal distribution with zero mean and
variance one.
It is constant, i.e. it is independent of t and ω. Processes with constant
tangent are
like staright lines and are in fact processes with homogeneous independent
increments.
Another example is the Posson process N(t) for which the tangent is of course
the Poisson
distribution.
Example 2: Markov processes have conditionals
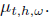that depend on ω only
through
x(t) = x(t, ω) and there is a map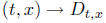 
that
defines the tangent.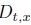 
is an infinitely
divisible distribution. Homogeneous transition probabilities correspond to
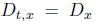
depending only on x.
Example 3: Continuous sample paths correspond to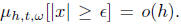
This is of
course the same as the Lindeberg condition that is needed for the limit to be
Gaussian. In
other words 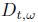being
Gaussian corresponds to continuos paths.
Example 4: Finally, if the process is Markov and has continuos paths then
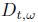is
Gaussian with mean b(t, x(t)) and variance a(t, x(t)). It is defined in
terms of the two
functions, a(t, x) and b(t, x). Homogeneous case corresponds to functions
that depend
only on x.
Example 5: The Gaussian processes are characterized
by linear regression and nonrandom
conditional variance. In this case the Gaussian measure
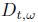with mean b(t, ω)
which is a
linear functional of the path x(s) : 0 ≤ s ≤ t and variance a(t) which is
purely a function
of t. If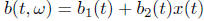 
then we should have a Gauss Markov
processes.
The question now is how to describe in mathematically precise terms the
relationship
between the process P and its tangent.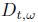
Let us look at Brownian motion as an
example.
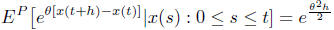
or
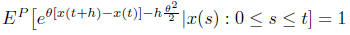
Equivalently
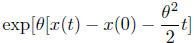
is a martingale w.r.t P and the natural filtration
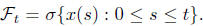The converse
that the only process P with respect to which the martingale property is valid
for all θ ∈ R
is Brownian motion is not hard to prove. From the martingale relation it follows
that
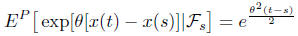
which implies that x(t) − x(s) is conditionally
independent of 
and has a Gaussian
distribution with mean zero and variance t − h. This makes it Brownian motion.
Lecture 2.
We will now discuss processes with independent increments. We are familiar with
Brownian
motion whose increments over intervals of lenth
are normally distributed with mean 0 and
variance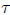 . More
generally the distribution of the increments of a procees with independent
increments over an interval of length
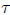will be a family
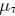of probability distributions such
that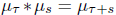 
where ∗ denotes convolution. Such
distributions are of course infinitely
divisible and possess the Levy-Khintchine representation for their
charecteristic function.
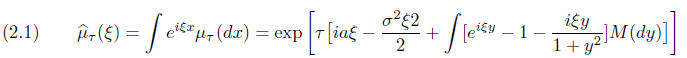
Here M(dy) is a sigma-finite mesure supported on R\0,
which can be infinite only near 0.
In other words
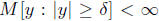for any δ > 0. More over M cannot be too singular
near 0. It must integrate y2.
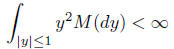
the characteristic function of an indpendent sum is the
product of the charecteristic func-
tions, the Levy-Khintchine representation of the new process, which is the sum
of the two
original processes is easily obtained by adding the exponents in (2.1). In
partcular we can
try to understand the process that goes with
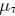by breaking up the
exponent into pieces.
If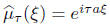
a then the process is deterministic with
x(t) ≡ at with probability 1. It is a
straightline with slope a. The slope is often called the ”drift”. But it
does not necessaily
imply that in general E[x(t)] = at.
If
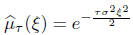
then process x(t) is seen to be Brownian motion with
variance σ2t. It can be represented
as σβ(t) in terms of the canonical Brownian motion with variance 1.
Before we turn to the final component that involves M let us look at the
canonical Poisson
process N(t). This is a process with independent increments such that the
distribution
of N(t) − N(s) is Poisson with parameter t − s. Since the increments are all
nonnegative
integers, this is a process N(t) which increases by jumps that are integers. In
fact the
jumps are always of size 1. This is not so obvious and needs a calculation . Let
us split the
interval [0, 1] into n intervals of length 1/n and ask what is the probability
that at leat one
increment is atleat k. This can be evaluated as
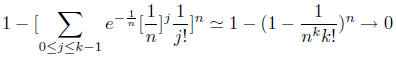
if k ≥ 2. This implies that the jumps are all of size 1.
The times between jumps are
all independent and have exponential distributions. One can then visualize the
Poisson
process as waiting for indpendent events with exponential distributions and
counting the
number of events upto time t. Therefore
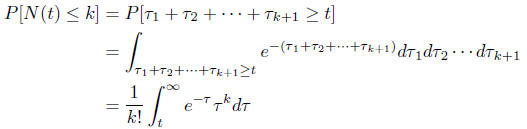
One can make the Poisson process more complex by building
on top of it. Let us keep a
sequence of i.i.d.random variables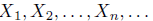 
ready and
define
so that instead of just counting each time the event
occurs we add and indpendent X to
the sum. We then get the sum of a random number of indpendent random variables.
The
characteristic function of X(t) is easy to compute.
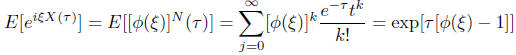
This is easily seen to lead to a Levy-Khintchine formula
with exponent
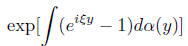
where α is the distribution of Xi. While slightly
diffrerent from the earlier form it can be
put in that form by writing it as
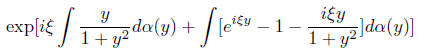
One should think of the Levy-Khintchine form as the
centered form where the centering
is not done by the expected value which will be by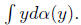
.
This may not in general
be defined. Instead the centering is done by a truncated mean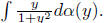
There is
nothin sacred about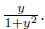 
One could have used any function θ(y) that looks sufficiently
like y near the origin and remains bounded near infinity. Notice that the
Poisson process
N(t) that enters the definition of x(t) can have intensity λ different from 1,
and nothing
significant would change except the final formula
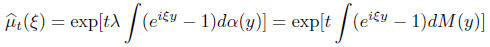
where now M is a measure with total mass λ. These are
called compound Poisson processes.
We can always decompose the σ-finite measure M as an infinite sum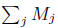
of finite
measures. then for the process X(t) with characteristic function
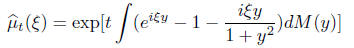
we have a representation as the sum
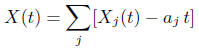
where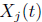
is the compound
Poisson process with Levy measure M, and the constants
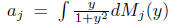are centering constants that may be needed.
Kolmogorov’s three
series theorem will guarantee that for the convergence of
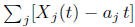it is necessary
and sufficient
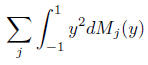
and
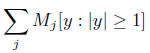
converge. Equivalently
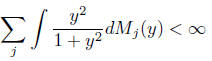
With out the centering the series may diverge and so it is
not possible to separate the two
sums
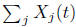and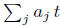
unless
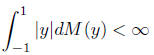
Remarks:.
If we add several mutually independent processes
with independent increments
their jumps cannot coincide. They just pile up at different times. Therefore for
any process
with independent increments X(t) the levy measure M has the interpretation that
for any
set A not containing the origin the number of jumps
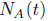in the interval [0, t] that are
from the set A is a Poisson process with parameter M(A) and for disjoint sets
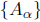, the
processes
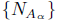are mutually independent. Except for the
centering that may be needed
this gives a complete picture of Poisson type processes with independent
increments. What
is left is a Process with independent increments with no jumps, which is of
course Brownian
motion with some variance σ2t and drift at.
Generators and Semigroups. A process with independent increments is a one
param-
eter semigroupμt of convolutions, i.e for t, s ≥ 0,
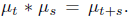On the space C(R)
of bounded continuos function on R this defines a one parameter semi group of
bounded
operators
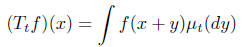
that satisfy
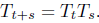Their infinitesimal generator
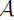is defined
as
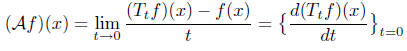
The general theory of semigroups of linear operator
outlines how to recover Tt from. Ba-
sically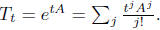
let us look at this for the Poisson
process.
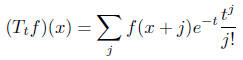
Simple differentiation gives
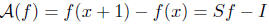
the difference operator, where S is the shift by 1. Then
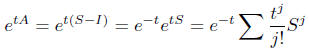
giving us the Poisson semigroup. For the Brownian motion
semigroup
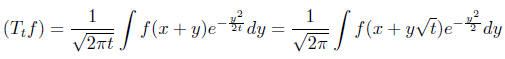
by a Taylor expansion of f, it is easy to see that for
smooth f
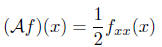
and for the deterministic process X(t) = at
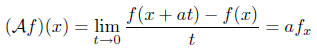
We can put all the pieces together and write for a general
process with independent incre-
ments represented in its Levy-Khintchine formula by [a, σ2,M], the
infinitesimal generator
is given by
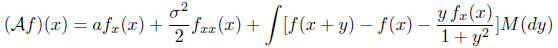
Among all process that commute with translations these
operators are singled out because
of two properties. One,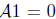 
,
beacuse μt are probability measures and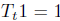 
.
Since
Ttf is nonnegative when ever f is, at the global minimum
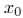of f(x), since f(x) ≥ f(),
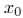it
follows that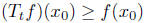 
for all t > 0. This means
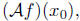, which is the maximum
principle. Any translation invariant operator with maximum principle satisfying
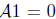
is given by a Levy-Khintchine formula.
The situation is much less precise if we allow
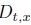to depend on t and
x(t). Now
instead of one Levy measure we have a whole family
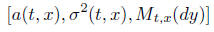
and infinitesimal generators that depend on t and do not
commute with translations.
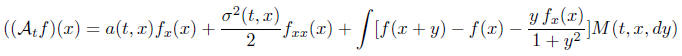
One of the more convenient ways of exploring the
relationship between the process and
the objects that occur in its representation is through a natural class of
functionals that
can be constructed from [a σ2,M] and P is characterized as the
measure with respect to
which these functionals are martingales.
