Matrix Operations
| |
Overview
 Definitions Definitions
 Addition Addition
 Norms Norms
 Matrix vector product Matrix vector product
 Naïve matrix product Naïve matrix product
 Alternative implementations Alternative implementations
 Blocking Blocking |
| Motivation Matrix Product
 Where matrix multiplication Where matrix multiplication
comes from?
 Let’s do some unscientific Let’s do some unscientific
computing
 Imagine you have lists of Imagine you have lists of
objects and of how many
components they consists of
 My car consists of a 3l-engine, 4 My car consists of a 3l-engine, 4
doors, 4 side windows, …
 Alex’s car consists of a 15lengine, Alex’s car consists of a 15lengine,
2 doors, 2 side windows,
…
 We can write this as a matrix? We can write this as a matrix?
 |
Motivation Matrix Product (ii)
 Now we have a 2nd list Now we have a 2nd list
 How the components are How the components are
composed of pieces
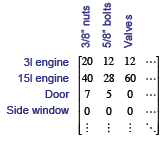
 The 3l engine contains 20 The 3l engine contains 20
3/8” nuts, 12 5/8” bolts, 12
valves, …
 One door contains 7 3/8” One door contains 7 3/8”
nuts, 5 5/8” bolts, 0 valves
 This leads us to a 2nd This leads us to a 2nd
matrix
 Now the stunning question: Now the stunning question:
How many 5/8” bolts
contains Alex’s car?
 |
| Motivation Matrix Product (iii)
 This is easy to compute This is easy to compute
 We multiply the number of We multiply the number of
components with the number of
pieces
 Then we sum this products over Then we sum this products over
all components
 Of course we can do this for all Of course we can do this for all
cars and all components
 So, we yield a 3rd matrix So, we yield a 3rd matrix
 Alex’s car contains 38420 3/8” Alex’s car contains 38420 3/8”
nuts, 7979034 5/8” bolts, 60
valves, …
 Jacob’s car contains … Jacob’s car contains …
 Such things you learn in Such things you learn in
vocational school not universities
 |
Definition Matrix Product
 Mapping Mapping
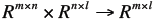
 For matrices For matrices
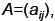
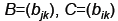
 The product C=AB is The product C=AB is
defined
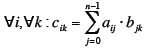
 |
| Operator Concatenation
 Recall matrices map from one vector space Recall matrices map from one vector space
to another
 Say B maps from V1 to V2 Say B maps from V1 to V2
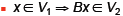
 Say A maps from V2 to V3 Say A maps from V2 to V3
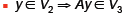
 Then AB maps from V1 to V3 Then AB maps from V1 to V3
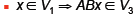
 Obviously dim(V2) = #rows(B) = #colums(A) Obviously dim(V2) = #rows(B) = #colums(A) |
Programming Matrix Product
 Computing dot product for all i and k: Computing dot product for all i and k:
double *a= new double[M*N], *b= new double[N*L],
*c= new double[M*L];
fill(&a[0], &a[M*N], 2.0); fill(&b[0], &b[N*L], 3.0);
fill(&c[0], &c[M*L], 0.0);
for (unsigned i= 0; i < M; ++i)
for (unsigned k= 0; k < L; ++k)
for (unsigned j= 0; j < N; ++j)
c[i*L+k]+= a[i*N+j] * b[j*L+k];
 Does the result change if we change the loops? Does the result change if we change the loops? |
| Changing Loop Order  No, any order yields correct results, e.g. k, j, i
No, any order yields correct results, e.g. k, j, i
fill(&c[0], &c[M*L], 0.0);
for (unsigned k= 0; k < L; ++k)
for (unsigned j= 0; j < N; ++j)
for (unsigned i= 0; i < M; ++i)
c[i*L+k]+= a[i*N+j] * b[j*L+k];
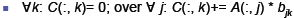
 One column of C is incremented by a column of A times scaled One column of C is incremented by a column of A times scaled
by an element of B
 This is called daxpy “double a⋅x plus y” This is called daxpy “double a⋅x plus y”
 Or saxpy for single precision, or caxpy for complex Or saxpy for single precision, or caxpy for complex
 Or gaxpy in general (generic?) Or gaxpy in general (generic?)
 Does this change our compute time? Does this change our compute time?
|
Run Time Analysis  Memory traffic
Memory traffic
 A: mn loads A: mn loads
 B: nl loads B: nl loads
 C: ml stores C: ml stores
 Operations Operations
 Multiplications: mnl Multiplications: mnl
 Additions: ml(n-1) Additions: ml(n-1)
 For simplicity , we consider m = n= l For simplicity , we consider m = n= l
 2n2 loads 2n2 loads
 n2 stores n2 stores
 2n3 operations (approximately) 2n3 operations (approximately)
 Is this what we really do ? Is this what we really do ?
|
| Run Time Analysis  We can’t store the whole matrix in processor
We can’t store the whole matrix in processor
 May be in cache? May be in cache?
 We have to reload values We have to reload values
 Even the values of C Even the values of C
 Unless we compute cik in the innermost loop Unless we compute cik in the innermost loop
 In reality we have In reality we have
 3n3 loads (instead of 2n2) 3n3 loads (instead of 2n2)
 n3 stores (instead of n2) n3 stores (instead of n2)
 2n3 operations 2n3 operations
 How many of them are from or to the memory? How many of them are from or to the memory?
 And how many from or to the cache? And how many from or to the cache?
 This depends on loop order This depends on loop order
|
n2 Vector Operations
| Variant |
Operation |
| i, j, k |
Gaxpy of row vectors |
| i, k, j |
Dot product |
| j, i, k |
Gaxpy of row vectors |
| j, k, i |
Gaxpy |
| k, i, j |
Dot product |
| k, j, i |
Gaxpy |
 All 6 variants are composed of vector operations All 6 variants are composed of vector operations
|
| Results for 500 by 500
> matrix_product 500
i, j, k = 2.78s, 89.9281 MFLOPS
i, k, j = 6.21s, 40.2576 MFLOPS
j, i, k = 3.18s, 78.6164 MFLOPS
j, k, i = 9.91s, 25.227 MFLOPS
k, i, j = 5.63s, 44.405 MFLOPS
k, j, i = 9.48s, 26.3713 MFLOPS
 Agai Agai o o a PowerBook G4 1.33GHz a PowerBook G4 1.33GHz |
Results for 512 by 512
> matrix_product 512
i, j, k = 2.87s, 93.5315 MFLOPS
i, k, j = 21.81s, 12.3079 MFLOPS
j, i, k = 3.46s, 77.5825 MFLOPS
j, k, i = 42.09s, 6.37765 MFLOPS
k, i, j = 22.51s, 11.9252 MFLOPS
k, j, i = 42.95s, 6.24995 MFLOPS
 Why is this so slow? Why is this so slow?
 Will explain this on the black board Will explain this on the black board |
| Results for 544 by 544
> matrix_product 544
i, j, k = 3.57s, 90.19 MFLOPS
i, k, j = 8.4s, 38.3308 MFLOPS
j, i, k = 4.04s, 79.6976 MFLOPS
j, k, i = 13.61s, 23.6575 MFLOPS
k, i, j = 7.35s, 43.8066 MFLOPS
k, j, i = 13.2s, 24.3923 MFLOPS
 This behaves like the first one (500×500) This behaves like the first one (500×500) |
544 by 544 with Single Precision
matrix_product 544
i, j, k = 2.17s, 148.377 MFLOPS
i, k, j = 4.28s, 75.2286 MFLOPS
j, i, k = 2.08s, 154.797 MFLOPS
j, k, i = 6.51s, 49.459 MFLOPS
k, i, j = 4.33s, 74.3599 MFLOPS
k, j, i = 6.36s, 50.6255 MFLOPS
 Twice as fast Twice as fast
 Because it takes half the time to compute or to load and Because it takes half the time to compute or to load and
store? |
| Row-Major Memory Layout
 Loop order (i, j, k) has unit-stride access but … Loop order (i, j, k) has unit-stride access but … |
Matrix Reload  Assume one matrix is larger than the cache
Assume one matrix is larger than the cache
 With loop order (i, j, k) With loop order (i, j, k)
 Matrix B is complete traversed in the 2 inner loops Matrix B is complete traversed in the 2 inner loops
 In next iteration of outer loop B is reloaded into In next iteration of outer loop B is reloaded into
cache
 Same with loop order (i, k, j) Same with loop order (i, k, j)
 With j as outer loop index we read C With j as outer loop index we read C
completely from main memory
 With k as outer loop index matrix A has to be With k as outer loop index matrix A has to be
reloaded
|
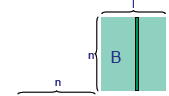
| Blocked Matrix Multiplication
 Assume we can Assume we can
partition A, B and C
into blocks of size L×L
 Then we can express Then we can express
the multiplication in
terms of vector
products of blocks
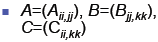
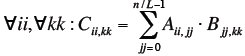

 |
What Do We Win?  If
block size is small enough, we can keep a block of If
block size is small enough, we can keep a block of
each matrix in cache
 Computation within the block loads from and stores Computation within the block loads from and stores
to cache
 After the first access to each element at least After the first access to each element at least
 Within the block we have Within the block we have
 3L2 loads from memory (at most) 3L2 loads from memory (at most)
 3L3 loads from cache, which are fast 3L3 loads from cache, which are fast
 L2 stores into memory L2 stores into memory
 L3 stores into cache, also fast L3 stores into cache, also fast
 2L3 operations 2L3 operations
 If L is large enough memory traffic is negligible! If L is large enough memory traffic is negligible!
 If L is too large blocks do not fit into cache :-( If L is too large blocks do not fit into cache :-(
|
| Program Blocked Matrix Product
fill(&c[0], &c[NS], 0.0);
for (int ii= 0; ii < blocks; ++ii)
for (int jj= 0; jj < blocks; ++jj)
for (int kk= 0; kk < blocks; ++kk)
for (int i= ii*B, i_end= (ii+1)*B; i < i_end; ++i)
for (int j= jj*B, j_end= (jj+1)*B; j < j_end; ++j)
for (int k= kk*B, k_end= (kk+1)*B; k < k_end; ++k)
c[i*N+k]+= a[i*N+j] * b[j*N+k];
 What other improvements can we make? What other improvements can we make? |
Blocking of 544 by 544 Matrices
> blocked_matrix_product 544 32
i, j, k = 1.27s, 253.526 MFLOPS
i, k, j = 1.75s, 183.988 MFLOPS
j, i, k = 0.94s, 342.53 MFLOPS
j, k, i = 1.11s, 290.071 MFLOPS
k, i, j = 1.77s, 181.909 MFLOPS
k, j, i = 1.26s, 255.538 MFLOPS
 Is there more we can improve? Is there more we can improve? |
| Unrolling Inner Loop
for (unsigned ii= 0; ii < blocks; ++ii)
for (unsigned jj= 0; jj < blocks; ++jj)
for (unsigned kk= 0; kk < blocks; ++kk)
for (unsigned i= ii*B, i_end= (ii+1)*B; i < i_end; ++i)
for (unsigned j= jj*B, j_end= (jj+1)*B; j < j_end; ++j)
for (unsigned k= kk*B, k_end= (kk+1)*B; k < k_end; k= k+4) {
unsigned index_a= i*N+j, index_b= j*N+k, index_c= i*N+k;
c[index_c]+= a[index_a] * b[index_b];
c[index_c+1]+= a[index_a] * b[index_b+1];
c[index_c+2]+= a[index_a] * b[index_b+2];
c[index_c+3]+= a[index_a] * b[index_b+3];
} |
Unrolling Dot Product
for (unsigned ii= 0; ii < blocks; ++ii)
for (unsigned kk= 0; kk < blocks; ++kk)
for (unsigned jj= 0; jj < blocks; ++jj)
for (unsigned i= ii*B, i_end= (ii+1)*B; i < i_end; ++i)
for (unsigned k= kk*B, k_end= (kk+1)*B; k < k_end; ++k) {
real_type tmp0= 0.0, tmp1= 0.0, tmp2= 0.0, tmp3= 0.0;
for (unsigned j= jj*B, j_end= (jj+1)*B; j < j_end; j= j+4) {
unsigned index_a= i*N+j, index_b= j*N+k;
tmp0+= a[index_a] * b[index_b];
tmp1+= a[index_a+1] * b[index_b+N];
tmp2+= a[index_a+2] * b[index_b+2*N];
tmp3+= a[index_a+3] * b[index_b+3*N]; }
c[i*N+k]+= tmp0 + tmp1 + tmp2 + tmp3; } |
| Results of Optimization
 Unrolling of scaled vector addition already done by Unrolling of scaled vector addition already done by
the compiler, no speedup here
 Constant index computation didn’t pay off either Constant index computation didn’t pay off either
 Unrolling dot product accelerated Unrolling dot product accelerated
 About 630 MFLOPS = ~ 1 double op. per 2 cycles About 630 MFLOPS = ~ 1 double op. per 2 cycles
 With single precision 650 MFLOPS With single precision 650 MFLOPS
 We can compute double precision and single precision at We can compute double precision and single precision at
almost the same speed
 Given they are already in cache Given they are already in cache
 If you want get faster use optimized libraries If you want get faster use optimized libraries |
More Variants  What
if we consider 2 levels of cache? What
if we consider 2 levels of cache?
 We need 9 loops We need 9 loops
 With 3 levels of cache we need 12 loops, … With 3 levels of cache we need 12 loops, …
 Dual concept: the nesting is not part of the algorithm Dual concept: the nesting is not part of the algorithm
but of the data structure / memory layout
 Morton-ordered matrices Morton-ordered matrices
 Prof. Wise will give a lecture about it Prof. Wise will give a lecture about it
 Unrolling Unrolling
 Mostly done by compiler Mostly done by compiler
 Superscalar dot products Superscalar dot products
 There are very fast libraries for this There are very fast libraries for this
 Most popular is BLAS Most popular is BLAS
 Often optimized by computer vendors Often optimized by computer vendors
|
| Why is Matrix Product so Important?
 Top 500 list of fastest computers is based on
Linpack Top 500 list of fastest computers is based on
Linpack
 Contains linear algebra algorithms Contains linear algebra algorithms
 Most of the time is spent in matrix products Most of the time is spent in matrix products
 If one can speedup up (dense) matrix product by If one can speedup up (dense) matrix product by
17% one gets a 17% better rating in Top 500
 Interest in fast dense matrix products is more Interest in fast dense matrix products is more
political then scientific
 What is more important? What is more important?
 Compute something people need, see next lectures Compute something people need, see next lectures |
|
Start solving your Algebra Problems
in next 5 minutes!
 |
 |
 |
|
Algebra Helper
Download (and optional CD)
Only $39.99
|
|
Click to Buy Now:
OR
|
|
|
 |
 |
 |
|
2Checkout.com is an authorized reseller
of goods provided by Sofmath
|
|
Attention: We are
currently running a special promotional offer
for Algebra-Answer.com visitors -- if you order
Algebra Helper by midnight of
January 22nd
you will pay only $39.99
instead of our regular price of $74.99 -- this is $35 in
savings ! In order to take advantage of this
offer, you need to order by clicking on one of
the buttons on the left, not through our regular
order page.
If you order now you will also receive 30 minute live session from tutor.com for a 1$!
|
You Will Learn Algebra Better - Guaranteed!
Just take a look how incredibly simple Algebra Helper is:
Step 1
: Enter your homework problem in an easy WYSIWYG (What you see is what you get) algebra editor:
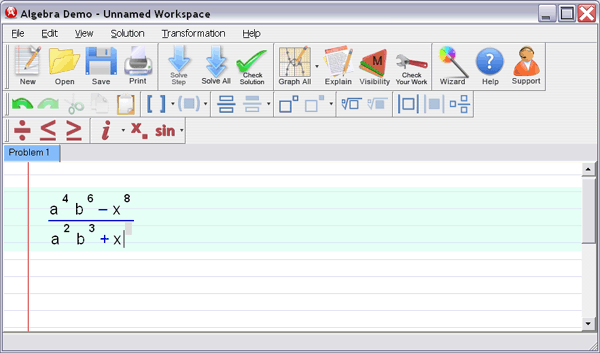
Step 2 :
Let Algebra Helper solve it:
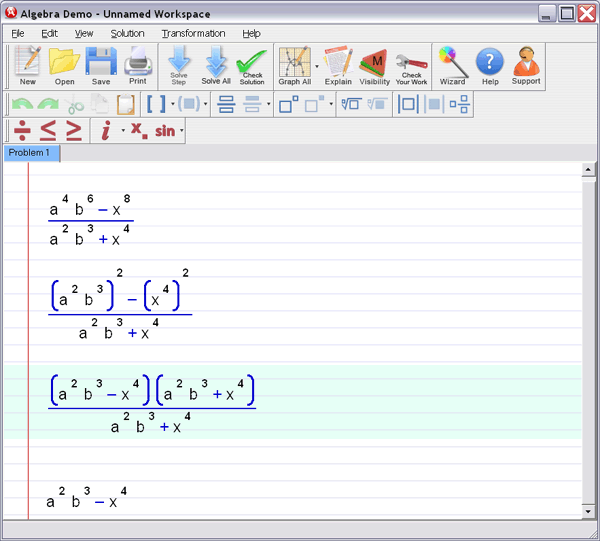
Step 3 : Ask for an explanation for the steps you don't understand:
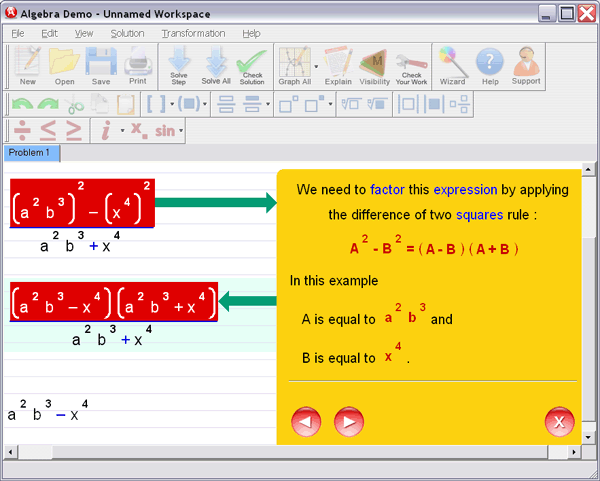
Algebra Helper can solve problems in all the following areas:
- simplification of algebraic expressions (operations
with polynomials (simplifying, degree, synthetic division...), exponential expressions, fractions and roots
(radicals), absolute values)
- factoring and expanding expressions
- finding LCM and GCF
-
(simplifying, rationalizing complex denominators...)
- solving linear, quadratic and many other equations
and inequalities
(including basic logarithmic and exponential equations)
- solving a system of two and three linear equations
(including Cramer's rule)
- graphing curves (lines, parabolas, hyperbolas, circles,
ellipses, equation and inequality solutions)
- graphing general functions
- operations with functions (composition, inverse, range, domain...)
- simplifying logarithms
- basic geometry and trigonometry
(similarity, calculating trig functions, right triangle...)
- arithmetic and other pre-algebra topics
(ratios, proportions, measurements...)
ORDER NOW!
 |
 |
 |
|
Algebra Helper
Download (and optional CD)
Only $39.99
|
|
Click to Buy Now:
OR
|
|
|
 |
 |
 |
|
2Checkout.com is an authorized reseller
of goods provided by Sofmath
|
|
|
 |
| |
| "It
really helped me with my homework. I was
stuck on some problems and your software walked me
step by step through the process..." |
| C. Sievert, KY
| |
| |
 |
| |
Sofmath
19179 Blanco #105-234
San Antonio, TX 78258
|
Phone:
(512) 788-5675
Fax: (512) 519-1805
| | |



