Section 6.1
1. For the given data the interpolation polynomial will be
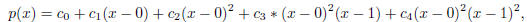
and the Newton tableau is
.
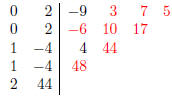
Hence the polynomial is
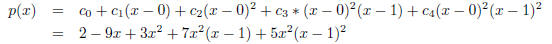
2. With additional data p(3) = 2 the polynomial shall be
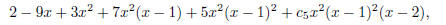
and the expanded Newton tableau is
.
The new polynomial is then
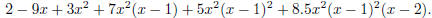
5. Plug x0, x1 into Eq.(10) one can readily check that p(x0) = c00, p(x1) = c10.
Taking derivative
of Eq.(10) we can get
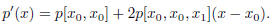
Plug x0 into this derivative we can find that p0(x0) = p[x0, x0] = c01.
9.
Proof. Since f interpolates g at x0, · · · , xn and h interpolates 0 at these
nodes, we know that
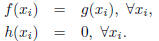
But then
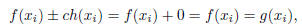
meaning that f ± ch interpolates g at the given nodes.
16. It is easy to check that p(a) = a, p(b) = b. We will be focused in checking
p'(x). Notice that
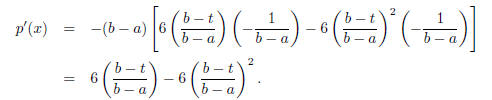
Thus p‘((a + b)/2) = 3/2, p’(a) = 0, p‘(b) = 0. Notice also that p’(t) is a
quadratic function with
negative leading coefficient , so p‘(t) has a maximum value at the t0 such that
p‘’(t0) = 0, i.e.,
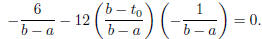
But then t0 = (a + b)/2, the middle point of the interval (a, b),
meaning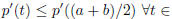 
(a, b). Since p'(a) = 0, p'(b) = 0, we know that p'(x) >= 0 in (a, b). Thus
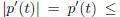
p'((a + b)/2).
6.4
1,2. Answers were given in class.
5. f(x) is a quadratic spline function because
• f(x) is a polynomial of degree less than or equal to 2 in
.
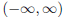• f(x) is continuous in 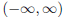. This can be check the value of f (x) at the ends
of each
subintervals.
• f0(x) is continuous in 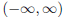. This can be check the value of
'f(x) at the
ends of each
subintervals.
6. Piecewise polynomial f (x) can be a cubic spline function only if
• f(x) is a polynomial of degree less than or equal to 3 in
.
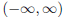• f(x) is continuous in 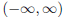. In particular, f(x) must be continuous at the
ends of each
subintervals.
• f0(x) is continuous in 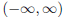. In particular, f'(x) must be continuous at the
ends of each
subintervals.
• f00(x) is continuous in 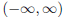. In particular, f''(x) must be continuous at
the ends of
each subintervals.
By examining these four criterions we get constraints for a, b, c, d, e, i.e.,
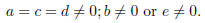
Since f(1) = 7, we know c = a = 7. Furthermore, from f(0) = 26 we get b = 2 and
from f(4) = 25,
we get e = −3.
