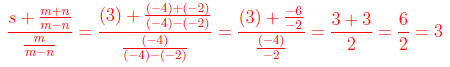Answers:
1. What is the product of −4 and −8?
Answer: 32 Remember that the product of two negative
numbers is positive, and the product
of a negative and a positive is negative.
2. What is 28 ÷ (−7)?
Answer: −4 The properties for dividing positive and
negative numbers is the same as for
multiplication.
3. What is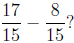 
Answer: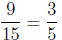
Adding and
subtracting fractions with the same denominator is easy. Here,
we have 17 fifteenths and we’re subtracting 8 fifteenths, which leaves 9
fifteenths. The Math
Placement Exam is a multiple choice test, and the correct answer may not be in
reduced
form.
4. What is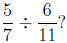 
Answer: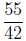
Multiplying and
dividing fractions is also easy. To multiply, you multiply the
numerators and you multiply the denominators. In this case, we are dividing by
6/11, which
is equivalent to multiplying by 11/6. In other words, we invert and multiply.
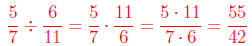
5. Simplify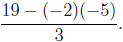 
Answer: 3 Remember to use the standard order of operations
(grouping symbols, then
exponents and radicals , then multiplication/division, and finally addition and
multiplication.
In this case, the division bar tells us to compute the numerator and denominator
before
dividing. In the numerator, we do the multiplication first, to get 19 − 10,
which simplifies
to 9. Finally, 9 divided by 3 equals 3.
6. What is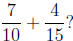 
Answer: 29/30 To add these fractions, we must first
convert both fractions so that they have
the same denominator, which in this case can be 30. This gives us
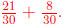This is now
similar to problem 3, and we get 29/30.
7. Round 177.546811 to three decimal places (that is,
round to three digits
to the right of the decimal point.)
Answer: 177.547 To round correctly, we look at the next
digit. If the next digit is 5 or more,
we round up. Otherwise, we round down. In this case, the next digit is 8, so we
round the
6 up to 7.
8. Convert 0.3547 to a fraction.
Answer: 3547/10000 Remember that the digits to the right
of the decimal point represent tenths,
hundredths, thousandths, etc. In this case, the fourth digit represents
ten-thousandths, and
we have 3,547 of these ten-thousandths.
9. Evaluate the expression x2 − 5x + 3 for x = −1.
Answer: 9 It’s a good idea to always substitute into
parentheses. Here, we get (−1)2 −
5(−1) + 3 = 1 + 5 + 3 = 9.
10. Write the following without parentheses −3(x2 − 3x +
4).
Answer: −3x2+9x−12 We’re distributing here, and the −3
must be multiplied times every
term inside the parentheses.
11. Multiply out (x − 3)(x + 5).
Answer: x2 + 2x − 15 Some would call this FOIL-ing. In
general, when multiplying poly-
nomials by polynomials, we multiply every term in the first factor times every
term in the
second. Here, we get x · x + x · 5 + (−3) · x + (−3) · 5 = x2 + 5x − 3x − 15 =
x2 + 2x − 15.
12. Multiply out (x − 5)2.
Answer: x2 − 10x + 25 The result of this is a perfect
square trinomial, which we know will
take a special form. Alternatively, we can simply multiply (x−5)(x−5) as we did
in problem
11.
13. Simplify x4 · x3.
Answer: x7 Here, we have 4 factors of x times 3 factors of x, which is 7
factors altogether.
Symbolically, when we multiply exponential expressions with the same bases, we
add the
exponents.
14. Simplify (x3)5.
Answer: x15 Here, we have 3 factors of x multiplied 5 times, which is 15
factors altogether.
Symbolically, when we raise an exponential expression to another exponent, we
multiply
exponents.
15. Simplify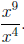 
Answer: x5 Here, we have 9 factors of x, and we are
dividing by 4 factors of x. This leaves
5 factors. Symbolically, when we divide exponential expressions with the same
bases, we
subtract exponents.
16. Simplify (−1)4.
Answer: 1 Remember that when multiplying an even number of
negative numbers together,
the result is positive. If there are an odd number of negatives, the result is
negative.
17. Solve the equation 3x + 4 = 10.
Answer: x = 2 When solving linear equations, we do the
same thing to both sides to try to
get x by itself on one side. In this case, we can subtract 4 from both sides to
get 3x = 6.
Then we divide both sides by 3 to get x = 2. At this point it is obvious that x
must be 2.
18. What is 50% of 70?
Answer: 35 A percent, like 50% can be thought of as a
fraction, 50/100 = 0.50. To find “a
percentage of ..., ” we multiply. In this case, we have 0.50 · 70 = 35. On the
Placement
Exam, you’ll need to be able to do this without a calculator .
19. Of x = −2, x = −1, x = 0, x = 1, and x = 3, which are
solutions to
the inequality 3x2 ≥ 12?
Answer: x = −2, 3 There are infinitely many solutions to
this inequality, but this question
is only asking which of these numbers are solutions. Plugging x = −2 into the
left side, we
get 3(−2)2 = 12, which is equal to, and therefore greater than or equal to, 12,
so x = −2 is
a solution. For x = −1, the left side is 3(−1)2 = 3, which is not greater than
or equal to 12,
so x = −1 is not a solution. Similarly, you will find that x = 0 and x = 1 are
not solutions,
and x = 3 is a solution.
20. Simplify | 7 − 11 |.
Answer: 4 You can think of an absolute value as being a
distance from zero, and as a result
must be zero or positive . In this case, we have | 7 − 11 | = | − 4 | = 4.
21. Graph the equation −2x + 5y = 10.
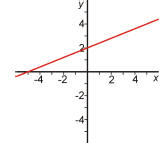
Answer: a.
To graph a line, you need to find at least two points on the line (i.e., two
solutions to the
equation). Two easy points take the form (0, y) and (x, 0). For (0, y), if we
substitute into
the equation, we get −2(0) + 5y = 10, which becomes 5y = 10 and y = 2. The point
(0, 2),
therefore, is a point on the line. Similarly, you can find that (−5, 0) is also
a point on the
line. Plotting these two points and drawing a straight line through them, gives
you the graph
shown above.
22. Graph the equation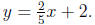 
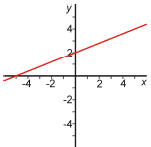
Answer: a.
This equation can be graphed as in problem 21, but this equation is in
“slope-intercept”
form, y = mx+b. In this case, we know that b is the y-intercept, so (0, b) = (0,
2) is a point
on the line. Since the slope is m = 2/5 , we can count from the y-intercept “up
2, right 5” to
find another point, (5, 4). Drawing the line through these points gives you the
graph. The
line is the same as the one from problem 21, but on the Placement Exam, this
won’t be the
case.
23 What is the slope of the line pictured?
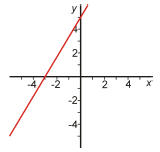
Answer: m = 5/3 The slope is the change in y over the
change in x between any pair of points
on the line. Looking at the graph, the easiest point to see are (0, 5) and (−3,
0). The change
in y is 0−5 = −5, and the change in x is −3−0 = −3. The slope, therefore, is
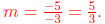
24. A distance of 1 inch represents 15 miles. If two
points on the ground
are 45 miles apart, how far are they apart on the map?
Answer: 3 inches Let’s say the distance we’re looking for
is x inches. The distances on the
map are proportional to the actual distances so x is to 45 as 1 is to 15. In
other words,
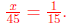Solving this equation yields x = 3.
25. Substitute m = −4, n = −2, and s = 3 into the
expression
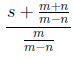
Answer: 3 Here, we simply substitute the values into the
expression and simplify. Be sure
to follow the order of operations .
