How many operations are needed for LU factorization?
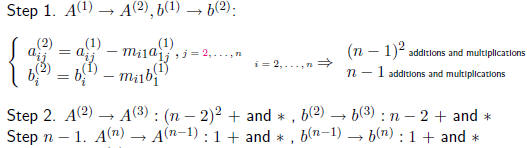
To get U = A(n) we need:
• Divisions :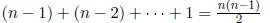
• Additions :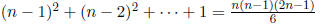
• Multiplications :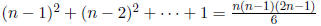
To get b(1) -> b(n) we need:
• Additions :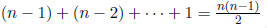
• Multiplications :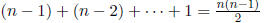
To solve Ux = g we need:
• Divisions : n
• Additions :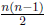
• Multiplications :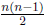
In total:
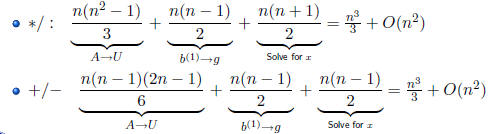
Conclusion: The cost of solving Ax = b is
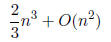
Note that if the size of the linear system doubles , the cost of only
factoring the matrix increases by a factor of 8.
If n is large, the principal cost in the solution of a linear system
Ax = b is the factorization A = LU.
Remark
In practice we need to solve Ax = b with varying vectors b:

•Cost of LU:
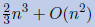
•Cost of back substitution :
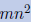
•Cost of forward elimination :
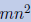
Total cost: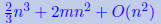
Computing A-1
Is equivalent to solving
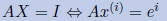
where x(i) is the ith column of A-1.
Hence the cost is (m = n):
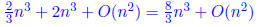
hence to compute
A-1 is 4 times more expansive than finding the solution of Ax
= b.