Problem 1. The volume of a sphere is proportional
to the cube of its radius. If a sphere of radius 10 cm has a volume of
4000 π/3 cm3, determine the formula for the volume of a sphere. Then, solve for
the radius in terms of the volume. Pay
attention to what is happening with the units.
Problem 2. The distance an object falls (neglecting wind resistance) is
proportional to the square of the time it falls. If
an object falls 176.4 m in 6 s, determine the formula for the distance an object
falls. Then, solve the formula for time.
Pay attention to what is happening with the units.
Problem 3. The kinetic energy of an object (energy of motion) is directly
proportional to the mass and directly
proportional to the square of velocity . If an object of mass 10kg moving at a
velocity of 8 m/s has kinetic energy
320 kg m2/s2 = 320 N, determine the formula for kinetic energy. Then, solve the
formula for the velocity. Pay attention
to what is happening with the units.
Problem 1. Rationalize the numerator in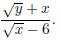
Problem 2. Rationalize the denominator in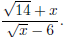
Problem 3. Rationalize the denominator in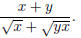
Try
to factor your final answer.
Problem 4. Rationalize the numerator in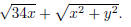
Problem 5. Rationalize the denominator in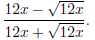
Try
to factor your final answer.
Problem 1. Solve the van der Waals equation (used to model
fluid compression in chemistry)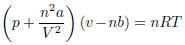
for p, and
then solve for a .
Problem 2. Solve the equation (used to model resistance in
electrical systems that have a temperature dependence)
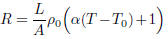for ρ0 and then solve for . The quantities ρ0
and T0 are labeled with subscripts in this equation.
Problem 3. Solve Graham’s law of effusion (used in
molecular chemistry)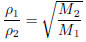
for M2, then solve for
M1.
Problem 4.Solve Archie’s law (used in geology to
measure conductivity of sedimentary rock)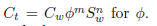
Here, the quantities Ct, Cw and Sw are labeled with subscripts. If you have a
brine saturated interval, then you can say
Sw = 1. What is the expression for in this case?
Problem 5. Solve Fitt’s law (used in human computer
interaction models)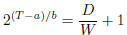
for D, and then solve for
W .
Sketching
Problem 1. Sketch 14x - 7y + 1 = 56.
Problem 2. Sketch x2 - 6x + y = 1.
Problem 3. Sketch the region that satisfies the inequalities x > y, y
≥3x2 -3x-8
and y < -4x+3. Don’t worry about
determining points of intersection–although you certainly could!
Problem 4. Sketch the line that is perpendicular to the line y = 3x + 4 that
passes through the point (1, 2).
Problem 1. Simplify so there are no negative exponents: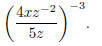
Problem 2. Simplify so there are no negative exponents: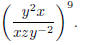
Problem 3. Simplify so there are no negative exponents: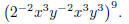
Problem 4. Simplify so there are no negative exponents
(write your final answer using exponents):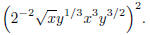
Problem 5. Simplify by distributing and write the final
answer using exponents instead of radicals: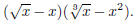
Problem 1. Combine to be a single fraction: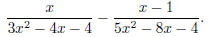
Problem 2. Solve for x if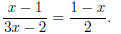
Problem 3. Solve for x if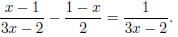
Problem 4. Solve for x if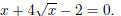
Problem 5. Divide the polynomial -20x3 + 33x2
-8x - 21 by
4x + 3.
Problem 6. What is the domain of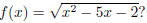
Problem 7. Solve for x if log2(5x + 1) − log2(x − 2) = 1.
Problem 8. What is the domain of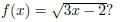
Problem 9. Solve for x if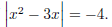
Problem 10. Solve for x if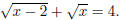
Problem 11. Solve the following equation for x: x4+ 4x2
-
1 = 0.
Problem 12. Solve the following for y: y-2+ 6y-1 + 4 = 0.
Problem 13. Solve the following for x: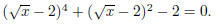
Other Problems
Problem 1. Write down the quadratic formula.
Problem 2. Derive the quadratic formula.
Problem 3. A right triangle has hypotenuse of length 3/4 cm and one side of
length 7/8 cm. What is the length of the
other side?
Problem 4. Factor x4 - 1.
Problem 5. Divide a3 + b3 by a + b using long division of polynomials, which
gives you the sum of cubes factoring rule:
a3 + b3 = (a + b)(a2 - ab + b2).
Problem 6. What is the distance between the two points (8,-7) and (-2, 1/4) in
the xy-plane?
Problem 7. What is the solution to the system of equations 4x - 5y = 10 and 5x
-7y = 9.
Problem 8. What is the solution to 12(x -3) -11(x -18) = x - 9?
