Sections
6.1 Rational Expressions and Functions : Multiplying and Dividing
6.2 Adding and Subtracting Rational Expressions
6.3 Complex Rational Expressions
6.4 Division of Polynomials
6.5 Synthetic Division and the Remainder Theorem
6.6 Rational Equations
6.7 Formulas and Applications of Rational Equations
6.9 Modeling Using Variation
6.1: Rational Expressions and Functions: Multiplying and Dividing.
Objectives:
1. To evaluate rational functions
2. To find the domain of a rational function
3. To interpret information given by the graph of a rational function
4. To simplify rational expressions
5. To divide rational expressions
A rational expression consists of a polynomial divided by a nonzero
polynomial.
Examples
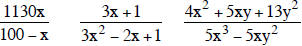
A rational function is defined by a rational expression.
Objective 1: To evaluate rational functions
Example: 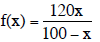
This function models the cost, f(x), in thousands of
dollars, to remove x%
of the pollutants that a city has discharged into a lake.
Find and interpret f(40).
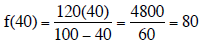
f(40) means it costs $80,000 to remove 40% of the lake’s
pollutants.
Look at the graph, Figure 6.1 page 376, in text. The graph illustrates that
the cost spirals upward as the percentages of pollutants removed increases.
Objective 2: To find the domain of a rational function
Look at the graph of 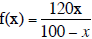 . on page 376 of
text.
. on page 376 of
text.
Question:
According to the graph, will the city ever remove all the pollutants
from the lake?
To do this, the city must remove 100% of the pollutants from the lake. The
answer is no.
The graph never touches the green broken line where x = 100%.
Note also that f is undefined when x =100%. This means that 100 can not
be in the domain of the function f.
The domain of a rational function is the set of all real numbers except those
for which the denominator is zero . To find the domain of a rational
function, set the denominator = zero and exclude value or values found.
Finding the domain.
Find the domain and write it using set-builder and
interval notation.
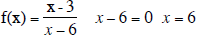
Domain: {x | x is any real number and x
 6} 0r (-∞, 6) ∪ (6, ∞)
6} 0r (-∞, 6) ∪ (6, ∞)
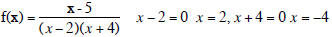
Domain: {x | x is any real number and x
 2, and x
2, and x  -4} 0r
-4} 0r
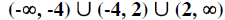
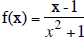 x2 is never
negative. So x2 is never = -1.
x2 is never
negative. So x2 is never = -1.
Domain: {x | x is any real number} 0r (-∞,∞)
Look at the graph of 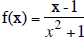 . [-4, 4] by [-2,
1]
. [-4, 4] by [-2,
1]
 |
x can be any real
number. |
Objective 3: To interpret information given by the
graph of
a rational function.
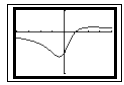
Graph 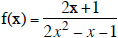
Observations:
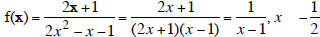
1. x
 -1/2 and x
-1/2 and x
 1
1

 See
graph below
See
graph below
2. Graph has two breaks -hole at x = -1/2 and x = 1.
3. Graph consists of 2 different branches . Each branch approaches but
never touches the dashed line x = 1.
4. The line x = 1 is called a vertical asymptote. The curve approaches the
line x = 1 but never touches it.
5. As x approaches infinite, the curve approaches the x-axis. As x
approaches negative infinite , the curve approaches the x- axis. The x-axis
or y = 0 is a horizontal asymptote. A curve may touch or pass
through a horizontal asymptote.
Every rational function does not have a vertical
asymptote or
a horizontal asymptote.
Use the given graph, on page 385, for problems 17-26.
Problem 18: Find f(1). f(1) = -1
Problem 19: What is the domain and range of f?
Domain: {x| x is any real number except 2 and –2}
Range: (-∞, 0] U (3,∞)
Problem 20: What are the vertical asymptotes?
The vertical asymptote are x = 2 and x = -2.
Problem 22; Describe the end behavior of the graph at the far
right. What is the equation of the horizontal
asymptote?
On the far right, the curve approaches the line y = 3.
The equation of the horizontal asymptote is y = 3.
Problem 24: Explain how the graph shows that f(2) does not exist.
The vertical asymptote at x = 2 shows that f(2) does not exist.
Problem 26. List two real numbers that are not function values of
f.
Any real number between 0 and 3 are not function values of f. For
example 1 and 2, or 1 and 3. ( any real number between 0 and 3)
Objective 4: To simplify rational expressions.
A rational expression is simplified if its numerator and denominator have
no common factors other than 1 or -1.
Procedure for simplifying a rational expression
1. Factor the numerator and denominator completely
2. Divide both the numerator and denominator by the common factor.
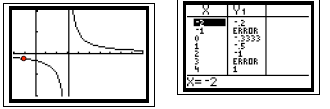
Simplify: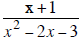
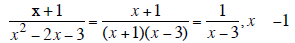
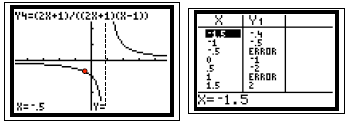
Look at the table 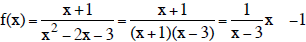
No y value when x = -1 or x = 3.
Show graph and table:
Hereafter, we will assume that a simplified rational
expression is
equal to the original rational expression, for all real numbers except
for those for which either denominator = 0.
Simplify: 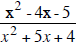
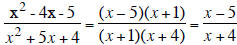
Do not have to indicate that x
 -1.
-1.
Simplify 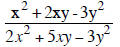
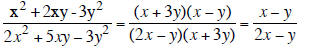
Simplify: 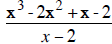
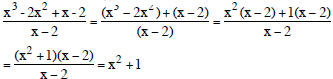
Objective 5: To multiply rational expressions
Rules:
1. Factor each numerator and denominator.
2. Divide numerators and denominators by factors common to both the
numerator and denominator.
3. Multiply the remaining factors in the numerators and multiply
the remaining factors in the denominators.
Multiply: 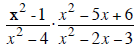
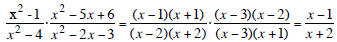
Multiply: 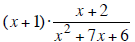
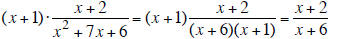
Objective 6: To divide rational expressions
The quotient of two rational expressions is the product of the first
expression and the reciprocal of the second expression
Divide: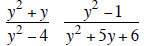
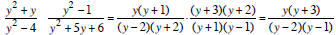
Divide: 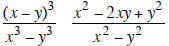
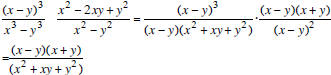
Use the given graph:
94. Find and interpret f(80). Identify your solution as a point on the
graph.
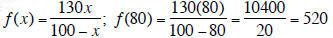
f(80) means that it will cost 520 millions of dollars to inoculate 80% of the
population.
The point on the graph is (80, 520)
Problem 96:
What happens to the cost as x approaches 100%. How is this shown by
the graph? Explain what this means.
As the x, the percentages of the population inoculated approaches 100%,
the cost continue to grow approaching infinite. 100% of the population
will never be inoculated, x cannot =100. X =100 is a vertical asymptote.



