1. Suppose that f is uniformly continuous on a set S
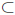R and 
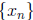is a Cauchy
sequence in
S. Prove that
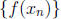is a Cauchy sequence. (f is not assumed to be continuous outside
S, so you cannot use Theorem 3.2, p. 60).
Proof. Let ε > 0. Since f is uniformly continuous on S, there exists
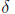> 0 such that
lx - yl < 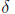implies l f(x) - f(y) l < ε
for all x, y ∈ S.
(1)
For this > 0 there exists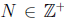
such that for n ,m > N,
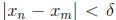. By (1) it
follows that for n, m > N,
.
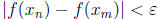Hence
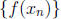is Cauchy.
2. Let M > 0 and let f : D → R, D
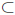R, satisfy the condition
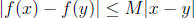for
all x, y ∈ D. Show that f is uniformly continuous.
Proof. Let ε > 0. Put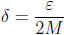 
. Then if
,
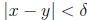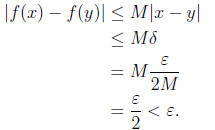
Hence f is uniformly continuous.
3. Suppose that for some constant M with 0 < M < 1,
,
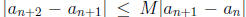n = 1, 2, 3,.... Prove that the sequence fang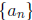 
is Cauchy.
Proof. We will first show that
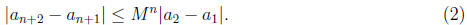
This is true for n = 1 as assumed. Suppose it is true for n = k. Then
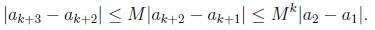
Hence (2) is true for all n.
For a fixed N and n = N + r, we have
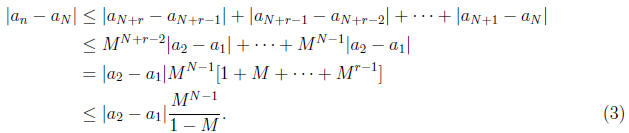
Given ε > 0, let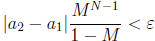 
. Then
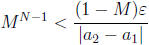. Take logarithms .
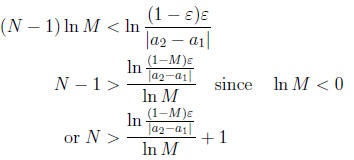
4. Suppose that f and g are continuous functions on the
closed interal [a, b] such that f(r) =
g(r) for every rational number r ∈ [a, b]. Prove that f(x) = g(x) for all
x ∈ [a, b].
Proof. Suppose that f(z) ≠ g(z) for some irrational number z in [a, b]. Let
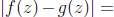
α. For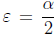 
, there exists
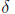> 0 such that
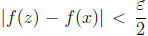and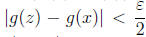 
whenever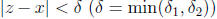 
. Let r be a rational number with
.
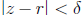Then
f(r) = g(r). Moreover,
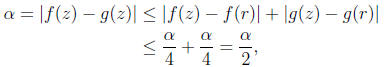
a contradiction. Hence f(z) = g(z) for all z ∈ [a,
b].
5. Let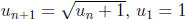 
.
(a) Show that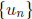 
is
bounded and monotone.
Proof. Let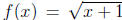
. Then
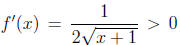for x > -1. Hence f is
increasing. Consider the point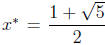 
. Then f(x*) =
x* . For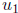 
= 1 < x* ,
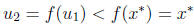. And by induction, we have
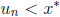. Hence 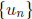is
bounded
above by x* . Since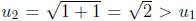 
, it follows by the same
reasoning that
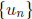is monotonically increasing. Hence by the
Bolzano-Weierstran Theorem,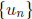
must converge.
(b) Find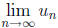 
.
Proof. Let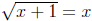 
. Then
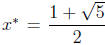is the limit point as
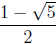is discarded
since it is negative .
6. Let S be the space of all rational numbers , with d(p, q) = l p - q l, and E
is the set of all
rational numbers p such that 2 < p2 < 3. Prove that
(i) E is closed and bounded.
(ii) E is not compact.
Proof.
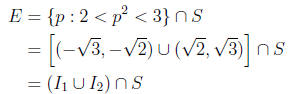
(a) E is clearly bounded by
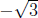and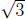 
. Let x ∈ E', then
there is a sequence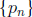 
in E with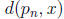 
→ 0 as n → ∞. Now
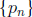is either in
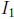or 
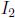, say
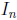. Hence
it
either converges in I, and hence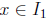 
or it converges to either
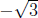or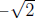 
which
are not in our space. Hence E is closed.
(b) Consider the open cover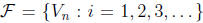 
where
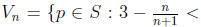
p2 < 3 }. This cover has not finite subcover. Hence it is not compact.
Another solution :
Take the sequence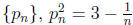 
. Then
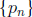has no
convergent subsequences.
7. Let E be a nonempty subset of a metric space (S, d). Define the distance from
x ∈ S to
the set E by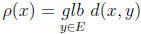 
.
(a) Prove that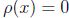 
if and only if 
.
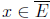(b) Prove that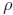 
: S → R is uniformly continuous on S.
Proof. (a) Let p(x) = 0. Then
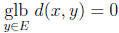. Hence there is a sequence
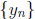in E
with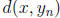 
→ 0 as n → ∞. Thus x ∈
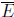. For the converse, let x ∈
.
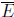If x ∈ E,
then as d(x, x) = 0, p(x) = 0. If x ∈ E\E, then there exists
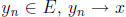as
n → ∞ or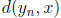 
→ 0 as n → ∞. Hence p(x) = 0.
(b) p : S → R. For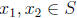 
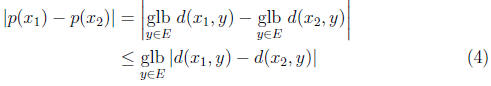
But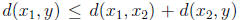 
or
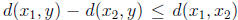. Similarly
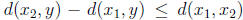. Thus 
.
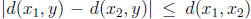Hence
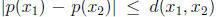. Given ε > 0, let
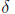= ε. If
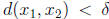, then
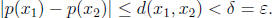
8. Suppose that f is continuous on an open interval I containing
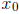, suppose
that f' is defined
on I except possibly at 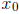, and suppose that 
.
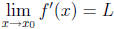Prove that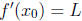 
.
Proof.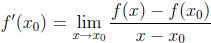 
if the limits exists. Since f is
continuous,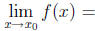 
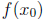. Now
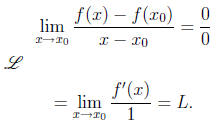
9. Let f and g be continuous functions on [a, b], g is
positive and monotonically decreasing
and g'(x) exists on [a, b]. Prove that there exists a point
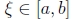such that
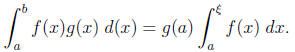
Proof. Let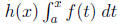 
. Since g is
positive , either
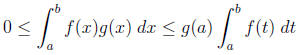
or
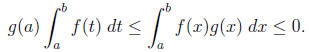
In either case,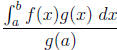 
is
between h(a) = 0 and h(b). By the Intermediate Value
Theorem, there exists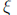 
between a and b such that
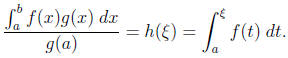
10. Suppose that f is continuous at x = a such that lf(a)l
< 1. Prove that there exists an
open interval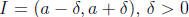 
, such that for all x ∈
I, l f(x) l ≤ M < 1, for some
fixed constant M.
Proof. Let L = l f(a) l < 1. If such an M does not exist for any
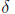, there exists a
sequence
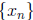that converges to a with
.
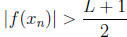Since f is continuous, 
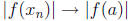as
n → ∞. But this is not possible as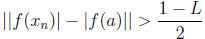 
for all n.
