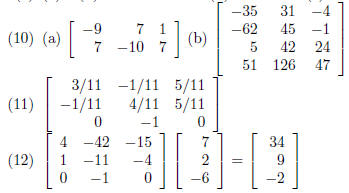Topics Covered on Exam 1
Section 1.2: Straight Lines
• Slope-intercept form of a line, y = mx + b, where
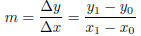and b is the y-intercept.
Section 1.3: Linear Function and Mathematical Models
• A function is a a rule or relationship that assigns to each input value one
and only one output value.
Note that two different input values can have the same output values, but a
unique input value
cannot have more than one output values.
Function notation: y = f(x) where x is the input and y is the output.
• Linear Cost, Revenue and Profit Functions
• Linear Demand and Supply Curves
Section 1.4: Intersection of Straight Lines
• Point of intersection of two given lines
• Break-Even Analysis
• Market Equilibrium
Section 1.5: Method of Least Squares
• Principle of Least Squares . The principle of least squares states that the
straight line that fits the
data points best is the one that minimizes the sum of the squares of d1, d2, d3,…, dn, that is,
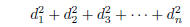
be made as small as possible. See page 52 of your text.
• You should know who the method of least squares works, but you do not have to
memorize the
normal equations given on page 53 of your text.
Section 2.1: System of Linear Equations: An Introduction
• Solve systems of two linear equations and two unknowns
• Express solutions of systems of equations with a unique solution, in¯nitely
many solutions, or no
solution
• Know the geometric interpretations of linear systems with a unique solution,
in¯nitely many solutions
and no solution
Section 2.2: Systems of Linear Equations: Unique Solutions
• Solve linear systems with unique solutions using the Gauss-Jordan elimination
method
- Allowed Gauss-Jordan row operations (see page 80)
- Gauss-Jordan Elimination method (see page 82)
Section 2.3: Systems of Linear Equations: Underdetermined and Overdetermined
systems
• Solve linear underdetermined and overdetermined systems using the Gauss-Jordan
elimination method
• Interpret solution from a row-reduced form of an augmented matrix (see page 79
of your text for the
meaning of a row-reduced form)
(1) Check the ¯nal matrix to see if there is no solution. (If the system has no
solution, state so and
stop here. Otherwise, go on to the next step )
(2) Check the leading 1s.
(a) If each variable has a leading 1 in its column, then there is a unique
solution.
(b) Otherwise, there are (potentially) multiple solutions and each variable not
having a leading
one in its column is a parameter.
• Overdetermined systems have more equations than unknowns. These systems can
have a unique
solution, infinitely many solutions, or no solution.
• Underdetermined systems have fewer equations than unknowns. These systems can
only have infin-
itely many solutions or no solution.
• If a system of equations has infinitely many solutions, you should represent
the solutions in parametric
form, e.g., with parameter t or s.
Section 2.4: Matrics
• Use matrices to represent data
• Addition and Subtraction Matrices
• Scalar Multiplication
Section 2.5 Multiplication of Matrices
• Multiplication of matrices
Section 2.6 The Inverse of a Square Matrix
• Find the inverse of a matrix
Practice Problems
In addition to these practice problems, you should be able to do and understand
your solutions to the
given homework problems, both online and written.
(1) Suppose the demand and price for strawberries are related by the
p(q) = 5 - 0.25q.
where p is the price (in dollars) and q is the supply (in hundreds of quarts) of
strawberries. How
much does demand have to increase for the price to decrease by $1.00?
(2) The manager of a restaurant found that the cost to produce 100 cups of coffee
is $11.02, while the
cost to produce 400 cups is $40.12. Assume the cost C(x) is linear function of
x, the number of cups
produced.
(a) Find the formula for C (x).
(b) What is the fixed cost?
(3) The table below shows the number of books checked out from a town library by
local residents from
1995 through 1999.
| Year |
1995 |
1996 |
1997 |
1998 |
1999 |
| Books (in thousands) |
412 |
476 |
538 |
601 |
664 |
(a) Make a scatter plot of this data. The scale on your plot should be made as
large as possible
and your must label your axes.
(b) Draw an estimated regression by eye. You must draw your line as accurately
as possible with
a straightedge.
(c) Find the linear model (equation of your regression line drawn in part b.)
that is the best fit for
this data, with x equal to the number of years. after 1995.
(d) Explain why a linear equation is a reasonable model for this data.
(e) Use your linear model to predict the number of books that will be checked
out of the library in
2009.
(4) Determine the value of k for which the system of linear equations has no
solution.
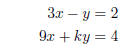
(5) Solve the system of linear equations using the Gauss-Jordan elimination
method.
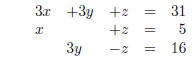
(6) The Coffee Shoppe sells a coffee blend made from two coffees, one costing $5/lb
and the other costing
$6/lb. If the blended coffee sells for $5.60/lb, find how much of each coffee is
used to obtain the
desired blend. Assume that the weight of the blended coffee is 100 lb.
(7) Suppose the augmented matrix for a linear system reduces to
Find the solution(s) of the system, they exist
(8) The accompanying figure shows the flow of down traffic during the rush hours on
a typical weekday.
Each road can handle up to 1500 vehicles/per without causing congestion. The flow
of traffic is
controlled by traffic lights at each of the five intersection.
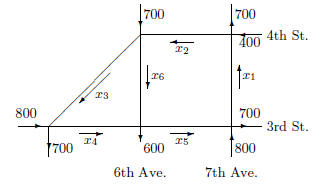
Set up a system of linear equations describing the traffic flow and solve this
system.
(9) A small publishing house specializing in poetry has a
fixed cost of $525 to
produce a typical volume.
The cost to produce 1000 copies of the book is $2675 in addition to the fixed
cost. The publisher is
able to sell each book for $4.95.
(a) Find the cost function for the book production .
(b) How many books must the publisher produce and sell to break even?
(c) How many books must the publisher produce and sell to make a profit of
$1,000?
(d) How many more books must publisher produce and sell to make increase their
profit by $100?
(10) Perform the indicated operations
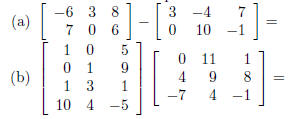
(11) Find the inverse of the matrix, if it exists
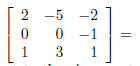
(12) Write the matrix equation that is equivalent to the given system of linear
equations, then solve the
system using the inverse of the coefficient matrix .
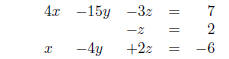
Answers. (No guarantees on correctness of answers)
(1) 4 quarts
(2) C(x) = 0.097x + 1.32
(3) f(x) = 62.9x + 412.4 is the line of best fit.
(4) k = -3
(5) x = 5, y = 16/3, z = 0
(6) 40lbs of the $5 blend and 60lbs of the $6 blend
(7) x1 = 4, x2 = -1, x3 = 3 - t, x4 = t
(8) The system as an augmented matrix
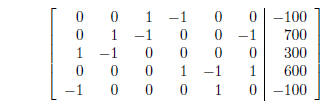
The system in row reduced form:
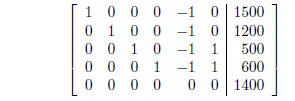
which means there's no solution to this system and this system of traffic light
doesn't work.
(9)
(a) C(x) = 2.675x + 525
(b) 231 books
(c) 671 books
(d) 44 books
