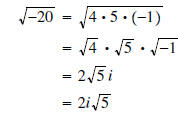Solving Equations

Solving Quadratic Equations

A quadratic equation is an equation that can be written in the form

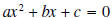
This is referred to as the standard form of a quadratic equation. We will discuss three methods for solving
quadratic equations: factoring, completing the square, and using the quadratic formula.

I. Solving by Factoring

The following theorem is the basis for solving equations by factoring :

Theorem: If ab = 0, then a = 0 or b = 0 or both.

Therefore, the following strategy can be applied to solve equations by factoring:

1. Write the equation in standard form (if it is not already in standard form)
2. Factor
3. Set each factor equal to zero and solve.

Example 1: Solve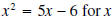

Solution: We first write the equation in standard form:
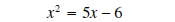subtract 5x from both sides

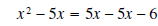
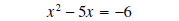add 6 to both sides

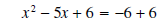
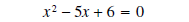now factor the left
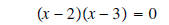set each factor equal to 0 and solve

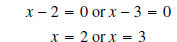
We can check both of our solutions:

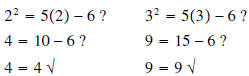
Both 2 and 3 are solutions.

Example 2: Solve

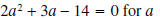
Solution: The equation is already in standard form, so factor and solve:

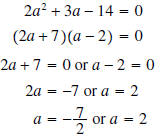
We can check both of our solutions:

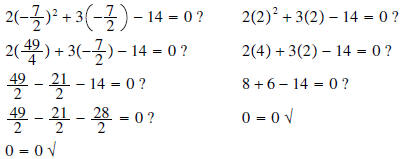
Therefore, both 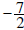and 2 are solutions to the equation .

II. Solving by Completing the Square

The equation x² = 9 can easily be solved by knowing that 3² = 9 (so x must be 3). However, there is another
number whose square is 9. Recall that the product of two negative numbers is a positive number. Thus
x = -3 is also a solution to the equation since

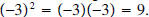
In general, the solution to the equation x² = c (where c is positive) is 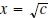or 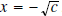.  This can be written
more concisely as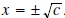 This method is often referred to as the square root extration method or simply the
square root method.

Example 3: Solve each of the following equations.

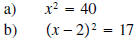
Solution:

a) The solution is given by (remember to simplify your radicals!)

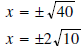
b) Note that if

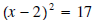
then

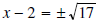
or (adding 2 to both sides)

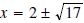
Given a quadratic equation 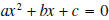(especially one which is not easily factored), we can rewrite the
equation so that the left-hand side is a perfect square (like the second example above). The process, which
works on every quadratic expression, is described below:

Example 4: Solve 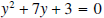by completing the square
Solution 1: We begin by arranging the left-hand side to look like

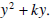
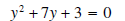subtract 3 from both sides

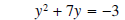
Now we half and square the linear coefficient (the number in front of y) and add this number to BOTH sides of
the equation:
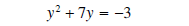add 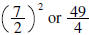to both sides
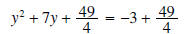get a common denominator on right
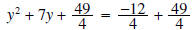add the numerators on right

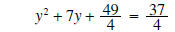
Why did we do this? Because the left-hand side is now a perfect square. Recall the special product

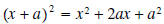
Notice that if we take one-half the coefficient of x and square it, we obtain

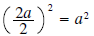
This will work no matter what a is.

Since the left hand side is a perfect square we can ”undo” the square by taking the square root of both sides.

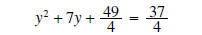“factor” the left
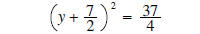now solve as example 2 above
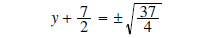simplify the radical
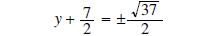subtract 7/2 from both sides
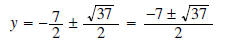final solution

Solution 2: Later it will be more useful when completing the square to organize our numbers as follows:

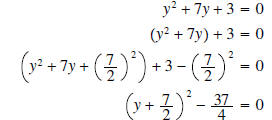
From here, we add 37/4 to both sides and continue as before.

Example 5: Solve 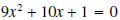by completing the square.

Solution 1: Since the coefficient of x² is not 1, we have to be more careful when writing the left-hand
side as

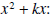
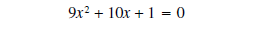subtract 1 from both sides
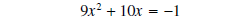divide both sides by 9
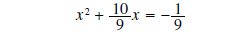half and square
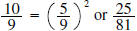
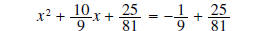common denominator on right
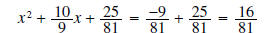factor left side (perfect square)
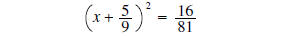solve using square roots
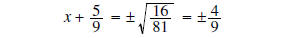subtract 5/9 from both sides

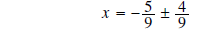
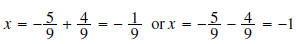
Solution 2: You must also be extremely careful if you use the alternate method of completing the square
here:

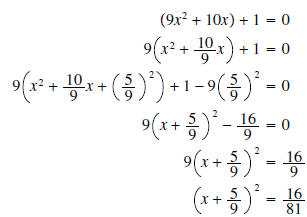
Then proceed as above.
Question: Why 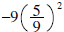in step 3?

Answer: We added the 5/9 inside the parentheses, so the 9 distributes over it:

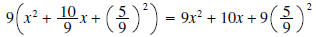
so we have actually added 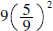to our expression. To balance this, we must subtract 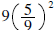from the
same side or add it to the other side.

III. Solving with the Quadratic Formula

We can use the technique of completing the square on the general quadratic equation 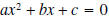to
derive a general formula for the solutions to a quadratic equation:

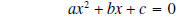	subtract c from both sides
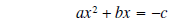	divide both sides by a
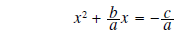	half and square
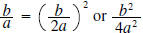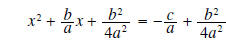	get a common denominator on right
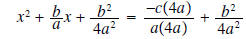	add numerators
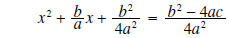	factor left side
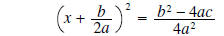	use square root method
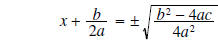	simplify radical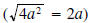
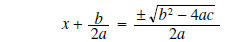	subtract b/2a from both sides
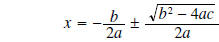	combine common denominator fractions

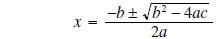The final step gives us the Quadratic Formula.

The solution to any quadratic equation of the form

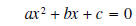
is given by

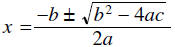
This formula must be memorized.

Remember: a is the coefficient of x², b is the coefficient of x, and c is the constant term in this formula.

Example 6: Solve 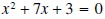using the Quadratic Formula
Solution: For the quadratic formula a = 1, b = 7, and c = 3.
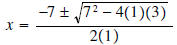substitute in formula

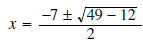
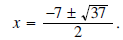. Thus, we have

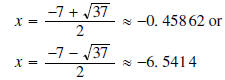
Example 7: Solve 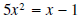using any method.

olution: First write the equation in standard form. The quadratic formula is generally the easiest
method to use when the quadratic does not easily factor.

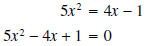
For the quadratic formula, 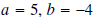(be careful with signs ), and c = 1.

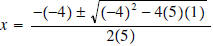
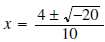simplify the complex radical (*See Note Below)
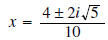now factor and cancel the common 2

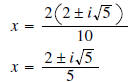
Note that the solutions above are complex numbers. Be sure to simplify any radicals in your final solutions!

*Note: In simplifying the complex radical, recall that

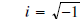
So