Some Remarks on the Teaching of Fractions in Elementary School

It is widely recognized that there are at least two major bottlenecks in
the mathematics education of grades K–8: the teaching of fractions and the
introduction of algebra. Both are in need of an overhaul. I hope to make
a contribution to the former problem by devising a new approach to elevate
teachers’ understanding of fractions. The need for a better knowledge of
fractions among teachers has no better illustration than the the following
story related by Herbert Clemens (1995):

Last August, I began a week of fractions classes at a workshop
for elementary teachers with a graph paper explanation of why
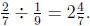The reaction of my audience astounded me. Several
of the teachers present were simply terrified . None of my protestations
about this being a preview, none of my “Don’t worry”
statements had any effect.

This situation cries out for improvement.

Through the years, there has been no want of attempts from the mathematics
education community to improve on the teaching of fractions (Lamon
1999, Bezuk-Cramer 1989, Lappan Bouck 1989, among others), but much
work remains to be done. In analyzing these attempts and the existing
school texts on fractions, one detects certain persistent problematic areas in
both the theory and practice, and they can be briefly described as follows:

(1) The concept of a fraction is never clearly defined in all of K–
12.

(2) The conceptual complexities associated with the common usage
of fractions are emphasized from the beginning at the expense
of the underlying mathematical simplicity of the concept.

(3) The rules of the four arithmetic operations seem to be made
up on an ad hoc basis, unrelated to the usual four operations on
positive integers with which students are familiar.

(4) In general, mathematical explanations of essentially all aspects
of fractions are lacking.

These four problems are interrelated and are all fundamentally mathematical
in nature. For example, if one never gives a clearcut definition of a
fraction, one is forced to “talk around” every possible interpretation of the
many guises of fractions in daily life in an effort to overcompensate. A good
example is the over-stretching of a common expression such as “a third of a
group of fifteen people” into a main theme in the teaching of fractions (Moynahan
1996). Or, instead of offering mathematical explanations to children
of why the usual algorithms are logically valid —a simple task if one starts
from a precise definition of a fraction,—algorithms are justified through ”connections
among real-world experiences, concrete models and diagrams, oral
language, and symbols (p. 181 of Huinker 1998; see also Lappan & Bouck
1998 and Sharp 1998). It is almost as if one makes the concession from the
start: “We will offer everything but the real thing”.

Let us look more closely at the way fractions are introduced in the classroom.
Children are told that a fraction c/d , with positive integers c and d, is
simultaneously at least five different objects (cf. Lamon 1999 and Reys et al.
1998):

(a) parts of a whole: when an object is equally divided into d
parts , then c/d
denotes c of those d parts.

(b) the size of a portion when an object of size c is divided into
d equal portions.

(c) the quotient of the integer c divided by d.

(d) the ratio of c to d .

(e) an operator: an instruction that carries out a process, such
as “2/3 of”.

It is quite mystifying to me how this glaring “crisis of confidence” in fractions
among children could have been been consistently overlooked. Clearly, even
those children endowed with an overabundance of faith would find it hard to
believe that a concept could be so versatile as to fit all these descriptions.
More importantly, such an introduction to a new topic in mathematics is
contrary to every mode of mathematical exposition that is deemed acceptable
by modern standards. Yet, even Hans Freudenthal, a good mathematician
before he switched over to mathematics education, made no mention
of this central credibility problem in his Olympian ruminations on fractions
(Freudenthal 1983). Of the existence of such crisis of confidence there is no
doubt. In 1996, a newsletter for teachers from the mathematics department
of the University of Rhode Island devoted five pages of its January issue to
“Ratios and Rational Numbers” ([3]). The editor writes:

This is a collection of reactions and responses to the following
note from a newly appointed teacher who wishes to remain anonymous:

“On the first day of my teaching career, I defined a rational number
to my eighth grade class as a number that can be expressed
as a ratio of integers. A student asked me: What exactly are
ratios? How do ratios differ from fractions? I gave some answers
that I was not satisfied with. So I consulted some other teachers
and texts. The result was confusion . . . ”

This is followed by the input of many teachers as well as the editor on this
topic, each detailing his or her inconclusive findings after consulting existing
texts and dictionaries (!). In a similar vein, Lamon (1999) writes: “As one
moves from whole number into fraction, the variety and complexity of the
siutation that give meaning to the symbols increases dramatically. Understanding
of rational numbers involves the coordination of many different but
interconnected ideas and interpretations. There are many different meanings
that end up looking alike when they are written in fraction symbol” (pp. 30–
31). All the while, students are told that no one single idea or interpretation
is sufficiently clear to explain the “meaning” of a fraction. This is akin to
telling someone how to get to a small town by car by offering fifty suggestions
on what to watch for each time a fork in the road comes up and how
to interpret the road signs along the way, when a single clearly drawn road
map would have done a much better job. Given these facts, is it any wonder
that Lappan-Bouck (1998) and Lamon (1999) would lament that students
“do” fractions without any idea of what they are doing? For example, it is
certainly difficult to learn how to add two “operators” in the sense of (e).

Sometimes one could “get by” a mathematical concept without a precise
definition if its rules of operation are clearly explained. Conjecturally,
that was how Europeans in the 14th and 15th centuries dealt with negative
numbers. In the case of fractions, however, this is not true even when interpretation
(b) of fractions is used. The worst case is the rule of adding two
fractions. In book after book (with very few exceptions, such as Lang (1988)),
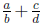is defined as (pa+cq)/m, where m = lcm{b, d} and m = bp = cq. Now
at least two things are wrong with this definition. First, it turns off many
students because they cannot differentiate between lcm and gcd . This definition
therefore sets up an entirely unnecesary roadblock in students’ path
of learning. Second, from a mathematical point of view, this definition is seriously
flawed because it tacitly implies that without the concept of the lcm
of two integers, fractions cannot be added. If we push this reasoning another
step, we would arrive at the absurd conclusion that unless an integral domain
has the unique factorization property, its quotient field cannot be defined.

Informal surveys among teachers consistently reveal that many of their
students simply give up learning fractions at the point of the introduction of
addition. It is probably not just a matter of being confused by gcd and lcm,
but more likely a feeling of bewilderment and disgust at being forced to learn
a new way of doing addition that seems to bear no relation to the addition of
whole numbers. This then brings us to the problem area (3) at the beginning
of this article. We see, for example, that Bezuk and Cramer (1989) willingly
concede that “Children must adopt new rules for fractions that often conflict
with well-established ideas about whole number” (p.156). In mathematics,
one of the ultimate goals is to achieve simplicity. In the context of learning,
it is highly desirable, perhaps even mandatory, that we convey this message
of simplicity to students. However, when we tell students that something
as simple as the addition of two numbers is different for whole numbers and
fractions, we are doing them a great disservice. Even when students are
willing to suspend disbelief and go along on such a weird journey, they pay a
dear price. Indeed, there are recurrent reports of students at the University of
California at Berkeley and at Stanford University claiming in their homework
and exam papers that 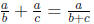and

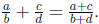
All in all, a mathematician approaching the subject of fractions in school
mathematics cannot help but be struck by the total absence of the characteristic
features of mathematics: precise definitions as starting point, logical
progression from topic to topic, and most importantly, explanations that
accompany each step. This is not to say that the teaching of fractions in
elementary school should be rigidly formal from the beginning. Fractions
should be informally introduced as early as the second grade (because even
second graders need to worry about drinking “half a glass” of orange juice!),
and there is no harm done in allowing children to get acquainted with fractions
in an intuitive manner up to, say, the fourth grade. An analogy may be
helpful here. The initial exploration of fractions may be taken as the “datacollecting
phase” of a working scientist: just take it all in and worry about
the meaning later. In time, however, the point will be reached when the said
scientist must sit down to organize and theorize about his or her data. So
it is that when students reach the fifth grade ([2]) or the sixth grade ([1]),
their mathematical development cannot go forward unless “miracles” such
as having one object c/d enjoying the five different properties of (a)–(e) above
are fully explained, and rules such as 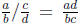justified. And it at this
critical juncture of students’ mathematical education that I hope to make a
contribution.