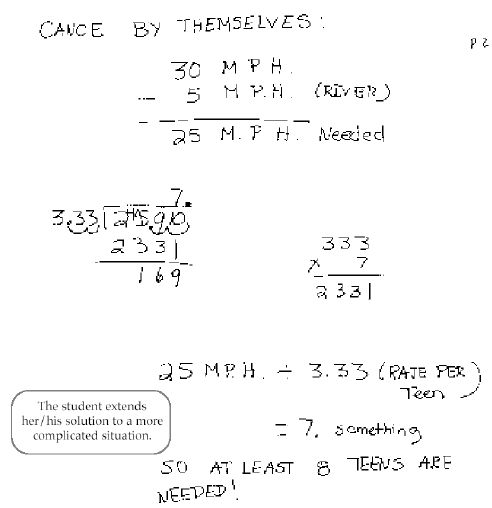Grade Level: 6 - 8
Task: Sink or Swim?
Standard: Patterns, Functions, and Algebraic Concepts
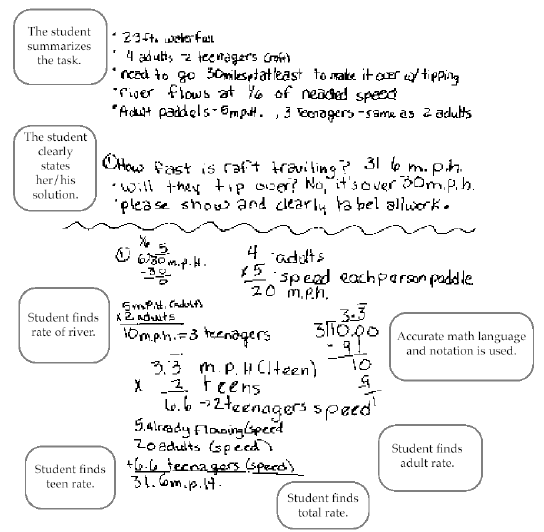
In New Zealand there is a river known as the Kaituna. On it, there exists a
23-foot
waterfall; some people like to go over the waterfall on a raft. A group of 6
people decide
to give it a try; they consist of four adults and two teenagers.
The raft MUST be traveling at least 30 miles per hour in order to successfully
go over
the falls; otherwise it will tip over. The river flows at one-sixth of the
needed speed. An
adult can paddle the raft at a speed of 5 miles per hour. Three teenagers can
paddle
the same speed as two adults.
How fast is the raft traveling?
Will the group be able to make it over the falls without tipping over?
Context – From the Task Author: This task was given at the end of the
school year
when rafting for recreation is on the minds of many middle level students.
What the task accomplishes…
This task allows the teacher to see the
students’ command of fractions and
decimals , and how students deal with repeated decimals.
What students will do…
Most students will start with what is easy, and work on the more challenging
parts
progressively. For instance, most students will easily see that the adults can
paddle
a total of 20 mph, but will then be slightly more challenged with finding the
1/6 of the
river speed.
The greatest challenge is in determining the rate of the teenagers, and
students will
come up with several different ways of doing so.
Finally students will interpret the remainder that results from their
calculations.
Time Required: 1 hour
Interdisciplinary Links: The task can be linked to units on boats, rivers, or to
the
recreational study of rafting. Students might enjoy attempting this task after
reading
Trouble River by Betsy Byars, and figuring out how long it might take the main
character
and his grandmother to travel down river.
Teaching Tips…
• In order to be successful with this task, students need experience with
dividing
whole numbers by fractional amounts, and with multiplying and dividing decimals .
• Students will also need experience with interpreting remainders.
Suggested Materials: Calculators
Possible Solution…
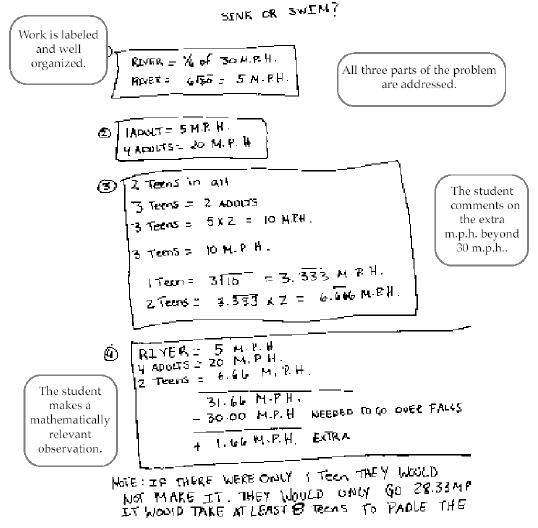
River travels 1/6 of 30 or 5 mph.
Adults paddle 5 mph x 4 adults = 20 mph.
3 teenagers paddle the equivalent of 2 adults or 2(5) = 10 mph.
1 teenager paddles (10 mph. รท 3) = 3.333, so 2 teenagers paddle 2 x 3.333 or
6.666
mph.
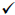The raft travels over the falls without trouble, since
their speed is greater than 30
mph.
Benchmark Descriptors:
The benchmark descriptors and rubric are designed to help the teacher analyze
student thinking and understanding at each of the four performance levels.
The descriptors are generalizations of what student work could look like.
It is not possible to anticipate every answer a student can give, so in
scoring student
work the teacher must use these generalizations to come to their own conclusions
as to where a student is performing on the assessment.
It is recommended that teachers create their own task specific rubric by
listing the
specific math skills that would make up each section of the four performance
levels.
Novice
The novice will show little or no understanding of the task.
Little of no math language will be used and no mathematical representation
will be
present.
No strategy for attempting to solve any part of the problem will be evident.
Apprentice
The apprentice may have a strategy for solving part but not the entire
problem.
The apprentice will use little math language and will not necessarily use
mathematical representations to communicate the solution.
The apprentice will show some correct reasoning, and some work will be
present.
Practitioner
The practitioner will have a strategy for addressing all parts of the problem
and will
achieve a correct answer.
The practitioner will use accurate and appropriate mathematical language and
notation and may use representations to communicate the solution.
Expert
The expert will successfully address all parts of the problem and may have a
sophisticated approach.
The expert will use precise mathematical notation and representations, as
well as
clearly explain the reasoning behind the decisions made.
The expert will use good problem solving strategies such as verifying his/her
solution
and will make other mathematically relevant observations.
APS Mathematical Standards…
The math standards stated for this task are aligned to the APS Draft
Standards 2000.
Strand – Number Sense and Operations :
Students will demonstrate number sense through experiences with meaningful
mathematical problems that focus on number meaning, number relationships, place
value concepts, relative effects of operations, and multiple representations to
communicate sound mathematical thinking.
Benchmark (6 – 8): The student will understand problems involving fractions,
decimals,
and percents and develop, analyze, and explain a variety of algorithms and
methods to
solve problems.
Performance Standards:
Sixth Grade:
• Select an appropriate operation to solve situational story problems.
• Select and use the appropriate number form (fraction, decimal, or percent) in
a
variety of situations, including measurement in U.S. and metric systems .
• Develop and test strategies for adding and subtracting fractions with like and
unlike
denominators .
• Develop and test strategies for multiplying and dividing fractions.
• Develop and test strategies for adding and subtracting decimals.
• Develop and test strategies for multiplying and dividing decimals.
• Estimate and solve problems involving fractions & decimals, and justify the
reasonableness of the solution.
Seventh Grade:
• Translate problem-solving strategies into efficient computation using
appropriate
mathematical terminology .
Eighth Grade:
• Select the appropriate representations to describe thought provoking real-life
situations.
• Manipulate all real numbers, their properties, and operations.
• Develop and evaluate arguments involving real numbers, their patterns and
operations.
• Develop and use strategies to estimate the results of rational-number
computations
and judge the reasonableness of the results.
Strand – Patterns, Functions, and Algebraic Concepts:
Students will demonstrate an understanding of algebraic skills and concepts
through
experiences with meaningful mathematical problems that focus on discovering,
describing, modeling, and generalizing patterns and functions, representing and
analyzing relationships, and finding and supporting solutions.
Benchmark (6 – 8): The student will use tables, graphs, and symbolic
representations
of patterns. The student will understand and use variable and linear equations
in
algebraic problem solving.
Performance Standards:
Sixth Grade:
• Solve one-step equations using the concept of balance when quantities are
added,
subtracted, or divided by both sides of an equation.
Seventh Grade:
• Identify and use variable expressions and formulas to solve a variety of
real-life
situations.
• Represent, describe, and analyze numerical patterns and linear relationships
using tables, graphs , words, and standard algebraic notation.
• Translate hypotheses into formal methods of solving algebraic equations.
Eighth Grade:
• Represent, describe, and analyze numerical patterns and linear relationships
using tables, graphs, words, and standard algebraic notation.
• Identify and model real-life situations using multiple representations.
• Develop and test strategies for solving multi-step equations.
Strand - Global Mathematical Processes:
Students will understand and use mathematical process.
Benchmark (K - 12): The student will use problem solving, reasoning and proof,
communication, connections, and representation as appropriate in all
mathematical
experiences.
Performance Standards:
Grades Kindergarten through twelve:
• Develops resourcefulness and perseverance in problem solving in mathematics
and
other disciplines.
• Recognizes when to use previously learned strategies to solve new problems.
• Develops and uses strategies for solving given problems.
• Monitors and reflects on the process of mathematical problem solving.
• Makes and investigates mathematical conjectures and use them successfully in
developing and evaluating mathematical arguments and proofs.
• Uses the concept of counterexample to test the legitimacy of an argument.
• Develops a logical sequence of arguments leading to a valid conclusion or
solution
to a problem (statement/reasons, proof, informal proof, and algebraic steps).
• Works in teams to share ideas, to develop and coordinate group approaches to
problems, and to share from each other in communicating findings.
• Relates applications to mathematical language in various modalities.
• Communicates mathematical thinking coherently and clearly to others.
• Analyzes and evaluates mathematical thinking and strategies of others.
• Identifies and connects functions with real-world applications.
• Identifies how seemingly different mathematical situations may be essentially
the
same (e.g. the intersection of two lines is the same as the solution to a system
of
linear equations).
• Investigates and explains the mathematics required for
various careers.
• Recognizes and applies mathematics in contexts outside the mathematics course.
• Develops a repertoire of mathematical representation that can be used
purposefully,
and appropriately interchangeably (e.g. pictures, written symbols , oral
language,
real -world situations, and manipulative models).
• Selects, applies, and translates among mathematical representations to solve
problems.
• Uses representations to model and interpret physical, social, and mathematical
phenomena.
Benchmark Papers
Notice
Apprentice
Practitioner
Expert
