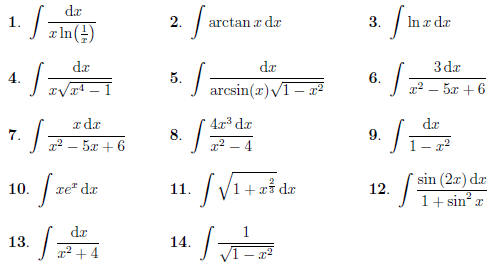1.6 Partial Fractions
Perhaps one of most difficult of the common techniques of integration to master
is the method of partial fractions. This method is almost exclusively used
in the cases of integrating rational polynomials, i.e. integrands of the form
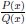. Partial fractions is used to split up the
integrand. If the degree of the
denominator is greater than 1, we may have trouble integrating it depending
on the degree of the numerator . Thus, we use partial fractions to split up
a single rational polynomial with a non -unity degree denominator into multiple
rational polynomials with more tractable denominators. Consider the
following situations:
• Deg[Q(x)]=1, Deg[P(x)]=0: In this case we can simply use the fact
that the integral of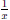 
is ln x
• Deg[Q(x)]=1, Deg[P(x)]>0: Here we can employ long division to break
this up into a regular polynomial plus a rational polynomial of the previous
form
• Deg[Q(x)]>1, Deg[Q(x)]>Deg[P(x)]: This case is the
classic partial
fractions situation. Here we can use partial fractions to split this rational
polynomial up into multiple rational polynomials that have lowerdegree
denominators that we can deal with individually.
• Deg[Q(x)]>1, Deg[Q(x)]<=Deg[P(x)]: First we must use long division
to obtain a regular polynomial and a rational polynomial that we perhaps
need to use partial fractions to split up further.
Let us illustrate an example of the third type. We seek to calculate
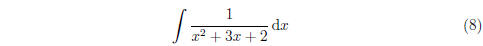
We notice that we cannot really use any of the techniques
we’ve learned
before to integrate this. But we can use partial fractions to manage this
rational
polynomial. We begin by factoring the denominator and then making
an educated guess as to what form this rational polynomial may split up
into:
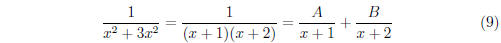
We have introduced constants A and B, which we need to
determine.
Notice that if it is possible to find such constants A and B that satisfy the
above equality, we can easily integrate the two terms on the right hand side.
But how do we determine the constants A and B? Let us rearrange (9) by
multiplying the entire expression by the denominator (x + 1)(x + 2):
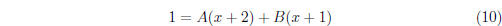
We now have a simpler algebraic relation which we can use
to determine
the constants A and B. Equation (10) must hold for all values of x and
because of this, we can match coefficients of like terms . That is, all the
terms multiplying x on the left hand side must sum to match the sum of all
the terms multiplying x on the right hand side, and all the constant terms
on the left must sum to equal the sum of the constants terms on the right
hand side. On the left hand side of (10) we have the polynomial 0x + 1 and
on the right hand side we have (A + B)x + (2A + B). From this we derive
two linear equations for A and B:
From these equations we determine that A = 1 and B = −1.
We have
thus been able to find constants A and B so that relation (9) is valid. We
can now rewrite (8) as follows:
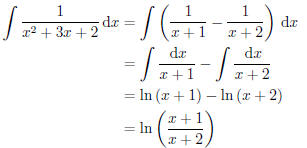
The modus operandi for partial fractions is pretty clear
and straightforward
once one is able to determine a reasonable guess for breaking up the
fraction (like in (9)). This step is the crucial step in the method. The key
is that you want to have as many unknowns as you have equations. If, after
getting to an equation like (10), we find too many equations or too many
unknowns, then we should back up to equation (9) to augment our guess.
Consider the following example:
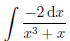
As before, we seek a guess for how to break up the
fraction:
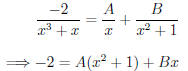
We now notice from the above equation that we have a
quadratic polynomial
equation, and thus we will have three constraint equations (one for
the x2 term, one for the x term, and a final one from the constant
terms).
However, we have only specified two unknowns, A and B. Therefore, unless
we are extremely lucky, we shall not be able to break up the fraction as we
have guessed. We therefore augment our guess as follows:
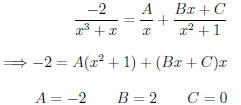
And now we may successfully perform the integration we
wish to accomplish.
1.7 Miscellaneous Techniques
There are many situations in which there simply are not any standard techniques
or methods for integration. Sometimes one just has to be a bit clever.
This section is devoted to such situations, and to other minor techniques
which are deemed to be deserving of notice. We start with some integration
results that are perhaps important enough to memorize:
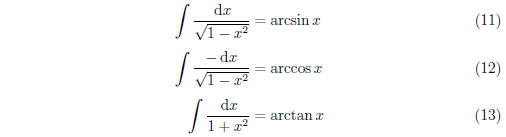
These formulas can be derived either by implicit
differentiation on the
functions arcsin x, arccos x, and arctan x, or by trigonometric substitution.
In any case, these formulas can perhaps save some time when one happens
across an integral of the above forms.
We illustrate other techniques via examples. Using the identity
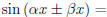
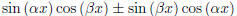
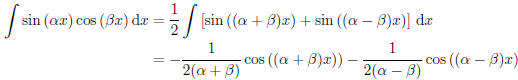
Another useful technique is completing the square.
Consider the following
integral and the solution method:
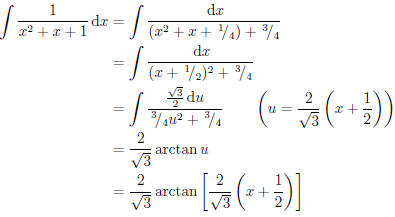
1.8 Exercises
Integrate the following expressions:
