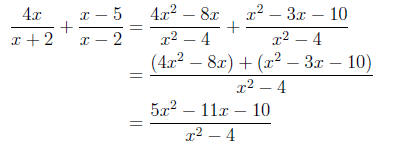A rational expression is a fancy word for a
fraction. A fraction has a top and a bottom. The
top is called the numerator and the bottom is called the denominator. Here is a
quick review on
how to add, subtract, multiply, and divide fractions. We'll begin with a review
of these operations
involving numbers, and then we'll move on how to handle these operations when we
have algebraic
expressions ( involving variables ).
1. Reduced and Non -Reduced Fractions: When working
with rational expressions, it is
always good express your answers in reduced form. What this means is to cancel
out any
common factors in the numerator and denominator. Below are some examples:
(a)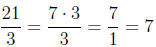
since 3 is factor of
the numerator and the denominator.
(b)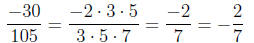
(c)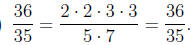
This is already
reduced.
When reducing fractions, it always helps to write both the
numerator and denominator in
factored form. This means write it as a product of numbers which can't be
factored any
further (prime numbers). Factoring the numerator and denominators will also be
useful
when finding the least common multiple.
2. Multiplication: Multiplying two fractions is
actually pretty easy. In this case trust your
instincts. The product of two fractions a/b and c/d is simply the product of the
numerators
over the product of the denominators:
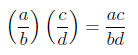
Don't get any of this confused with cross multiplication,
that comes into play in a whole
different context . Here are a few examples:
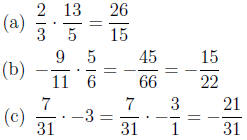
Notice all of the answers are written in reduced form.
3. Division: Dividing two fractions might seem more
complicated, but after one quick step,
it is the same as multiplication. Given any two fractions a/b and c/d , we
divide as follows:
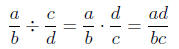
Dividing the two fractions is the same as multiplying the
first by the reciprocal of the second.
Here the order does matter, meaning
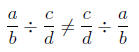
You should convince yourself why. Here are some examples:
4. Least Common Denominator: When adding or
subtracting fractions, you must first find
the least common denominator of the two fractions. Consider the following sum of
fractions :
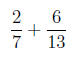
WE DO NOT ADD THE NUMERATORS AND THE DENOMINATORS!!! Before
you
start adding anything, first find a good common denominator. Here is a sure fire
way to
find a good common denominator which we can use to eventually add or subtract
any two
fractions a/b and c/d : the product of the two denominators (in this case the
product of b and
d) will always work as a good common denominator which we can use to add to
fractions
together. In the example above, a good denominator to use to eventually add the
fractions
together is the product of the two denominators, (7)(13) = 91.
Finding a good common denominator in the manner above
doesn't always find the best
common denominator. The best common denominator you can find is the least common
denominator. One way to define the least common denominator of two fractions is
the
smallest number for which both denominators divide (without a remainder). Here
is a sure
fire step by step process to find the least common denominator of two fractions.
Consider
the two fractions
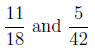
(a) First completely factor each denominator:
(b) Next note all of the factors the two denominators
share. In this example both 18 and
42 have 2 and 3 as factors.
(c) Compute the product of the two multiples. In our
example 18 * 42 = 756. This would
be a good common denominator to use to add the two fractions, but it is really
big , so
we will try to find the smallest common denominator.
(d) Finally, divide the product above by the common
factors we found in the second step
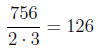
(e) Check that both denominators do in fact divide evenly
into the number above:
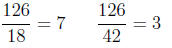
As you can imagine, it will be much easier to work with a
denominator of 126 rather than 756.
5. Addition and Subtraction: Adding and subtracting
fractions is much harder than multiplying
or dividing them. DO NOT JUST ADD THE DENOMINATORS AND ADD THE NUMERATORS!!
You can only add or subtract fractions once they have the same denominator.
Consider first when they do:
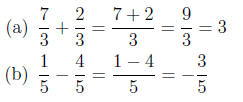
Recall that when adding or subtracting fractions which
have the same denominator, the
denominator does not change. We add or subtract the two numerators, and the
denominator
remains the same.
In order to add or subtract fractions, we must write them over the same
denominator first,
and therefore the first step in adding or subtracting fractions is to first find
the least
common denominator. Let's say wish to find the sum below:
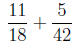
Follow these (not so simple) steps:
(a) Find the least common denominator. We did this in the
previous section, and we found it to be 126.
(b) Divide the least common denominator by each of the
denominators of the two fractions, and make a note of the quotient of each.
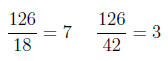
This means we need to multiply 18 by 7 to get 126, and we
need to multiply 42 by 3
to get 126.
(c) Note the following observations. Multiplying a number
by 1 doesn't change its value.
For any number a, a/a = 1, so multiplying a fraction by a/a (for any number
) won't
change its value. I guess this is not a step, but it is an observation we will
use in the
next step.
(d) We need to write each fraction over a common
denominator before we can add anything.
In light of everything above, in order to write the fraction 11/18 as a fraction
over a
denominator of 126,
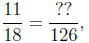
we know we need to multiply the denominator, 18, by 7 in
order to get 126. If we
multiply the numerator by 7 as well we won't change the value of the fraction :
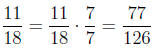
Next we do the same for the 5/42 only now we multiply both
the numerator and denominator by 3:
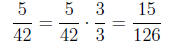
(e) Now that we have equivalent expressions for each
fraction both written over the least
common denominator of 126, we are ready to add the fractions:
To test yourself out, here is another example:
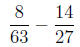
First note the least common denominator is
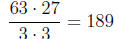
since 63 and 27 have two factors of three as a common
factors, and no other factors in
common. Next we write each fraction over the least denominator. Since 189
divided by 63
is 3, we will have to multiply the denominator 63 by 3 in order to get 189.
Similarly, since
189 divided by 27 is 7, we will have to multiply the denominator 27 by 7 in
order to get 189:
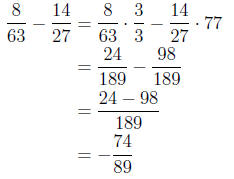
If you understand these ideas and operations with
fractions, then working with algebraic
expressions in the fractions is really no different. Let's revisit some the
ideas with some variables
mixed into things.
1. Reduced and Non-Reduced Rational Expressions: As
we did in working with numbers,
in order to reduce a rational expression we must factor both the numerator and
denominator
and cancel out any like factors . See the examples below:
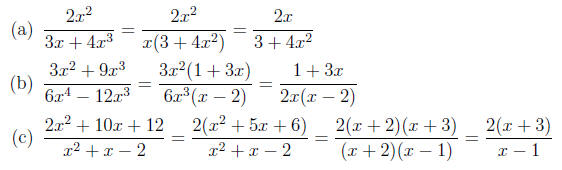
2. Multiplication: When multiplying two rational
expressions, the result will have a numerator
which is the product of the numerators of each fraction, and it will have a
denominator
which is the product of the denominators of each fraction. See the example
below:
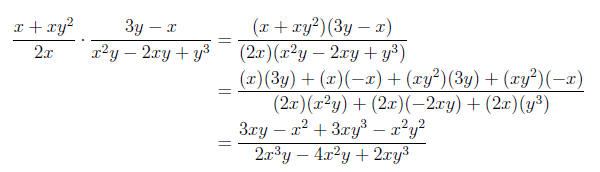
3. Division: In order to divide two rational
expressions, we take the product of the first
fraction and the reciprocal of the second fraction. Above we illustrated how to
take such a
product. So dividing two rational expressions involves one extra step of taking
the reciprocal
of the second expression. Remember it is important to note you must take the
reciprocal of
the second expression, not the first!
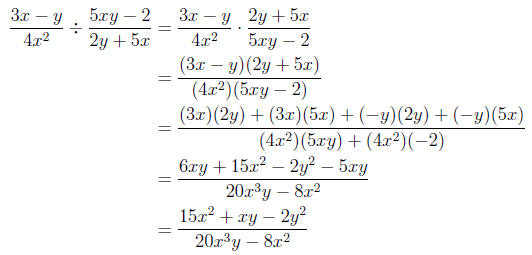
4. Least Common Denominator: In order to add two
rational expressions, the must first
be put over the same denominator. So again we must find the least common
denominator
of two rational expressions. Consider the two fractions below, and we'll walk
through the
steps to find a common denominator:
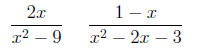
(a) Factor the denominators of each expression.
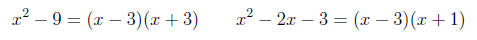
(b) Make a note of the factors which appear in both
denominators. In this example note
that the factor (x - 3) appears in both denominators.
(c) The least common denominator is the product of the two
denominators divided by
all of the common factors (which we found in the previous step). Therefore for
this
example the least common denominator is
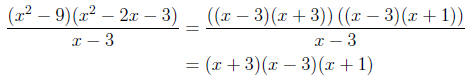
The first (x - 3) in the numerator is cancelled by the (x
- 3) in the denominator, but
the other (x - 3) still remains.
5. Addition and Subtraction: We can only begin to
add or subtract fractions once they are
over a common denominator. Once we have the two fractions over a common
denominator,
the numerator of the sum is the sum of the numerators, and the denominator does
not
change.
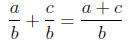
Below is an example of how to add rational expressions
which follows in the same fashion
as when adding fractions involving numbers only.
Example Simplify the sum
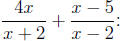
First we must find the least common denominator. The two
denominators x + 2 and x - 2
are already factored. They do not share any common factors (other than 1). The
least
common denominator is therefore the product of the two denominators (we don't
need to
divide by any common factors since there are none)
The Least Common Denominator is (x +
2)(x - 2)
Next we need to express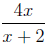
as
a fraction which over the denominator (x+2)(x-2).We
would have to multiply the denominator by (x - 2). In order keep the value of
the fraction
unchanged, we must multiply both the numerator and denominator by (x - 2):
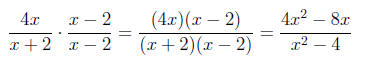
Similarly, in order to write the fraction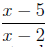
over the common denominator we must
multiply both the numerator and denominator by the factor (x + 2):
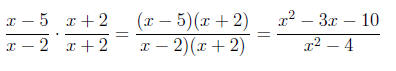
Finally we are ready to add the fractions now
that they are over a common denominator:
for
some 
