Section A. Each correct answer is worth 1 point.
1. Find the exact value of the average of the squares of the first six natural
numbers.
Solution :
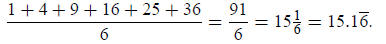
2. On the first test you scored 80. On the second test you scored 89. Find the
percent of increase
to the nearest hundredth of one percent.
Solution: The rate of change (increase or decrease) is:
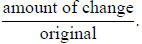
We have 9/80
= 0.1125. Then change to a percent (multiply by 100): 11.25%
3. Let a = log2 8; let b = log3 8. Find the value of a − b correct to the
nearest hundredth.
Solution: log2 8 is equal to 3, but finding log3 8 calls for a calculator and
the change-of-base
formula: logb x = log(x)/ log(b), where “log” is either the natural logarithm (ln)
or common
log (log10). On full-display calculators, you can type something similar to:
log(8)/log(2) - log(8)/log(3)
This gives 1.107210739; to the nearest hundredth, the answer is therefore 1.11.
4. Let sin θ = −5/7, with terminal side in quadrant IV. Write the exact value of tan θ.
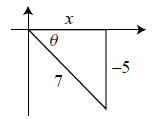
Solution: Use the Pythagorean theorem: 52+x2 = 72, so x2 = 24.
Since x is positive, we have
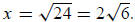Finally,
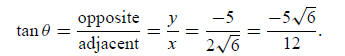
5. Name the author of the first geometry book, Elements.
Solution: Euclid (Greek, around 300 B.C.).
6. Otto’s Auto Rental charges $52 per day, and 32 cents per mile for an
automobile rental. Arnold
paid $578.40 to rent a car for three days. How many miles did he drive?
Solution: The cost equation is: Cost = 52 × days + 0.32 × miles.
Since he rented the car for three days, we can simplify the equation : C = 156 +
0.32m.
Then put in his cost: 578.40 = 156 + 0.32m.
And solve for m : 422.40 = 0.32m, so m = 1320 miles.
7. Find the domain of the function: f (x) = x2 − 2.
Solution 1 (algebraic): This function does not have:
1) square (or other even) roots of a negative number
2) division by zero
3) logarithms.
Consequently, there are no input values that cause any difficulty, so the domain
is all real numbers ,
or (−∞,∞).
Solution 2 ( graphing calculator ): The graph appears to extend in both the
positive and negative
x-directions forever. So we would guess that the domain is all real numbers.
(This does not
really prove that the domain is all real numbers, but it gives support for that
conclusion.)
Solution 3 (math knowledge): The domain of any polynomial is all real numbers.
Section B. Each problem is worth 2 points.
8. Write the equation of the line through (−3, 2) and perpendicular to the line
3x−y = 7. Express
your answer in slope- intercept form : y = mx + b.
Solution: There are many approaches to this problem. Here is one:
Put 3x − y = 7 in slope-intercept form: y = 3x −7. Its slope is 3; a line
perpendicular to it has
a slope of −1/3. So our equation has the form
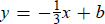. Temporarily substitute the point
(−3, 2): 2 = −1/3(−3) + b, or 2 = 1 + b. Therefore, b = 1, and the
equation is
.
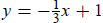9. The positive integers a, b, c are said to form a Pythagorean triple if a2 +
b2 = c2. Write two
distinct Pythagorean triples in the form a, b, c (with a < b < c) such that c =
65.
Solution 1 (a little algebra and trial & error): Solve for b2 and you get b2 =
c2 − a2. Then
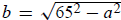. Now try different integers in place of a:
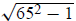is not an integer, nor is
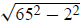, etc. The first triples you get this way are
16, 63, 65 and 25, 60, 65.
(There are two
other answers as well: 33, 56, 65 and 39, 52, 65.) The trial and error process
can be shortened
by using the table or list features on a graphing calculator.
Solution 2 (math knowledge): Notice that 65 = (5)(13), and note that these are
the hypotenuse
lengths for two familiar right triangles: 3-4-5 and 5-12-13. We can therefore
rescale the first of
these by a factor of 13, and get one triple: 39, 52, 65. The second triple comes
from scaling a
5-12-13 triangle by a factor of 5: 25, 60, 65.
10.
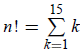. Write the value of n.
Solution:
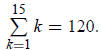You can do this quickly in a calculator; however, there is a formula:
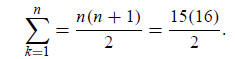
A little trial and error reveals the answer: 120 = 5!, so n = 5.
11. Find three numbers a , b, and c so that 2, a, b, c, 5 is an arithmetic
sequence.
Solution 1: The formula for the nth term of an arithmetic sequence is an = a1 +d(n
−1). Since
a1 = 2 and a5 = 5, we can find d (the difference):
5 = 2 + d(5 − 1)
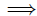5 = 2 + 4d
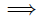3 = 4d
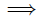d = 3/4
Then a = 2.75, b = 3.5, c = 4.25.
Solution 2: The average of the 1st and 5th terms is
b:
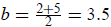. Likewise, a is the average
of 2 and b (the first and third terms), and c is the average of b and 5:
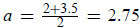and
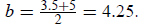
12. In a certain class of 60 students:
20 study German;
25 study Spanish;
18 study French;
5 study German and French;
9 study German and Spanish;
7 study Spanish and French;
4 study all three languages.
How many students are studying no language?
Solution: Use a Venn diagram. For example, observe that there are 4 students
taking all three
languages, and 5 studying French and German. Therefore, 1 student is taking
French and German
(but not Spanish). This leads to the numbers in the gray shaded area in the
diagram on the left.
Continuing in this way, we fill in the diagram and eventually arrive at the
figure on the right.
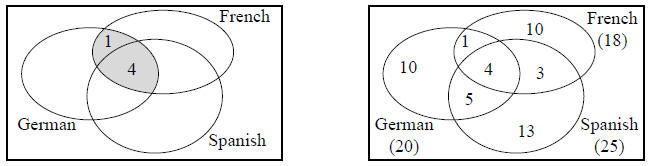
That’s a total of 10+10+13+1+5+3+4 = 46 students taking at least one language.
Thus
14 are not taking a language.
Section C. Each problem is worth 3 points.
13. From the top of a 200-ft-tall square water tower, SpongeBob observes a car
moving toward
the tower. If the angle of depression of the car changes from 25◦ to 50◦ during
the time of
observation, how far does the car travel (to the nearest foot)?
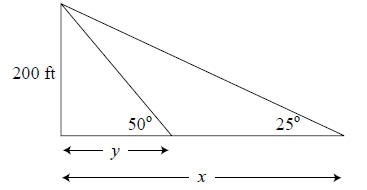
Solution: Angle of elevation always equals
the angle of depression, so we will work
with angle of elevation (it’s easier). In the
figure,
tan 25º = 200/x
x .=
428.9
tan 50º = 200/y
y .=
167.8
The distance traveled is x − y; to the nearest foot, the car travels 261 feet.
14. Given matrices
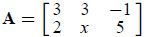and
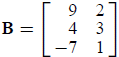. The value of the entry in the second
row, first column of matrix AB is 2003. Find x.
Solution: The second row, first column comes from multiplying row 2 of
A and
column 1 of B:
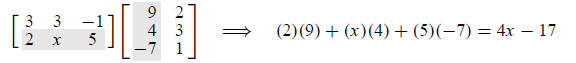
Set this equal to the given entry value and solve for x: 4x − 17 = 2003, so x =
505.
15. A right circular cone has the same volume as a sphere. If the base of the
cone has the same
radius as the sphere, find the height of the cone in terms of that radius r .
Solution: The volume of any cone is
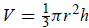. The volume of a sphere is
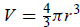. Since
they have the same volume, set the equations equal to each other (if the radii
were not the same,
we would need to use two different variables for r —perhaps r1 and r2.):
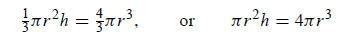
Now work on getting h by itself. There are many approaches; the most direct is
to divide both
sides by πr2, which leaves h = 4r .
