OBJECTIVES FOR THE MMPT

G. Functions

Be able to;

• tell whether a given relation is also a function

Ex. Is the relation { (x,y) | x² + y² = 4 } a function?

• given a function f(x), evaluate f(a) for some given value ‘a’
Ex.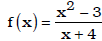. Evaluate f(-2).
• given a function f(x), simplify the expression :
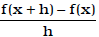
Ex. Given f (x) = x² + 2x − 3 , simplify the expression:

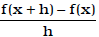
• find the domain and the range of a given relation or function

Ex. Determine the domain and the range of { (x,y) | y = x² − 4 };

• tell whether a function is even, odd or neither;

Ex. Is f(x) = x|x| an even, odd or neither function?

• perform operations with functions ( addition , subtraction, multiplication, division &
composition of functions) stating the domain of definition of the resulting function

Ex. Given 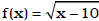and g(x) = x² + 5, evaluate (f o g)(3) ; Next, determine
(f o g)(x) and its domain;

• find the inverse of a given function

Ex. Find f ^-1(x) if ;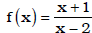

• Apply rigid &/or non-rigid transformations on the basic functions

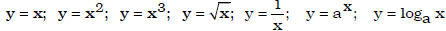to graph related functions,

or given the graph of functions obtained by applying rigid or non-rigid transformations,
determine their equation.

Ex. The graph of f(x) is the same as y = x² stretched vertically by a scaling
factor of 2, then shifted to the right 3 units and up 2 units. What is the
equation of f (x)?

H. Midpoint, Distance & Equations of Circles

Given the coordinates of two points A & B, be able to:

• determine the coordinates of the midpoint M of the segment

Ex. Given: A(-2,3), B(-6, 9). Determine the coordinates of the midpoint of ;

• determine the distance from A to B

Ex. Given: A(-2,3), B(-6, 9). Determine the distance from A to B;

Be able to:

• find an equation of the circle given its center and radius

Ex. The center of a circle is at C(2,-5) and its radius 6. Find the equation of the
circle.

• given the equation of a circle determine its center and radius

Ex. A circle has for equation: x² + y² − 6x + 8y − 75 = 0 . Determine its center
and radius.

• solve problems related to midpoint, distance and equations of circles.

I. Linear Functions

Be able to:
• find the slope of the line through two given points
Find the slope of the line through A(2,6) & B(-4,5);

• find the equation of a line given some of its properties or characteristics
Ex. Find an equation of the line with slope 4 and which passes through (2,7);

• determine whether two lines are parallel, perpendicular, or neither
Ex. Are the to lines 3x – 2y = 7 and 2x + 3y = 10 parallel? perpendicular?

• find the equation of a line parallel or perpendicular to a given line
Ex. Find the equation of the line that passes through (0,7) and is perpendicular
to the line whose equation is y = 4x – 5;

• find the coordinates of the point of intersection of two given lines
Ex. y = 2x + 3 and 5y – 2x = 4;

• find the equation and the slope (if any) of vertical or horizontal lines
Ex. Find the equation of the vertical line through (2,6). What is its slope?

• determine the x- & y- intercepts of a line , given it equation.
Ex. Find the x- & y- intercepts of the line 2x – 3y = 12.

J. Quadratic Functions

Be able to:
• determine the coordinates of the x- & y- intercepts of a quadratic function.
Ex. Determine the x- & y- intercepts of the function f (x) = 2x² − 3x − 5 ;

• express a quadratic function f (x) = ax² + bx + c in the form: f (x) = a (x − h)² + k

Ex. Express the function f (x) = 2x² − 8x + 3 in the form: f (x) = a (x − h)² + k ;

• determine the concavity of a quadratic function
Ex. Is the graph of the function f (x) = 2x² − 8x + 3 concave up or down?

• determine the coordinates of the vertex (the max or min) of a quadratic function
Ex. What are the coordinates of the vertex of f (x) = 2x² − 8x + 3 ?

• determine the maximum or minimum value of a quadratic function
Ex. What is the minimum value of the function f (x) = 2x² − 8x + 3 ?

• determine the domain and the range of a quadratic function
Ex. Determine the domain and range of the function f (x) = 2x² − 8x + 3 ;

• apply ones knowledge of the role that the sign of ‘a’, ‘ b² − 4ac ’, and ‘c’ play in the graph
of the parabola y = ax² + bx + c , to match the graph of parabolas with such
characteristics.

Ex. Which of the following parabolas has the following characteristics?

a>0, & b² − 4ac <0?

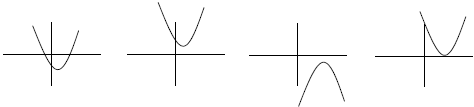
• match the graph of quadratic functions with their equation.
Ex. Refer to the 4 parabolas drawn above . Which of them could be the graph of
f(x) = −2x² + 4x − 4 ?