ALGEBRA, COMPUTER ALGEBRA, AND MATHEMATICAL THINKING

ABSTRACT

Mathematical symbolism generally-and symbolic algebra in particular -is among mathematics'
most powerful intellectual and practical tools. Knowing mathematics well enough to
use it effectively requires a degree of comfort and ease with basic symbolics. Helping students
acquire symbolic fluency and intuition has traditionally been an important, and sometimes
daunting, goal of mathematics education. Cheap, convenient, and widely available technologies
can now handle a good share of the standard symbolic operations of undergraduate
mathematics. differentiation, integration, solution of certain DEs, factoring and expansion
in many forms, and so on. Does it follow that teaching these topics, and even some of the
techniques, is now a waste of time?

The short answer is "no." On the contrary, as machines do more and more lower-level
symbolic operations, higher-level thinking and deeper understanding of what is really happening
become more, not less, important. Numerical computing has not made numerical
viewpoints obsolete, neither will computer algebra render symbolic mathematics obsolete.
The key question is how to help students develop that bred-in-the-bone "symbol sense" that
all mathematicians seem to have. What really matters is that students use mathematical
symbolism effectively to pose worthwhile problems in tractable forms. Once properly posed,
such problems are well on the way to solution, very often with the help of technology. The
longer answer, which I'll explore in the paper, concerns choosing mathematical content and
pedagogical strategies wisely in light of today's technology.

Introduction

What does it mean to know and do mathematics effectively at the tertiary level? How
do the answers reflect the present and future, when mathematical technology, including
symbol-manipulating technology, is already widely available, and will probably soon be
ubiquitous.

What should college-level students in particular know and what should they be able
to do, in order to be mathematically educated in a technology-rich environment? How
can we teachers help bring students to this kind of knowing?

I approach these questions from a perspective that's fairly common in the United
States. I'm a generalist mathematician who teaches reasonably pure mathematics to
North American college students. About one-third of my students in an average class
intend, with varying degrees of intellectual seriousness and interest, to complete a 4-
year mathematics major. Only a small minority (no more than 10%) of students plan
postgraduate study in mathematics. A more typical student plans to work after graduation
in a technical but not university-level academic job, such as software engineering,
database management, or high school teaching.

I am a practitioner, not an expert researcher in mathematics education, and so will
not presume to offer advice on the education research agenda or how it should be carried
out. What I do hope to contribute is a teacherly and mathematical perspective on what
content, techniques, and ideas related to symbolic mathematics I think are mathematically
most important to a modern tertiary student clientele, and how I think students
can be helped-often with technological assistance-to acquire these advantages.

1 The technology background

Disputes over educational uses of mathematical technology have been around as long
as the technology itself. Years ago one heard the "desert island" argument from opponents
of instructional technology. Students who use calculators for school arithmetic
might suffer disproportionately if later shipwrecked on low-tech islands. This argument
is seldom heard anymore, it was killed either by the rising availability of cheap calculators
or by the worldwide decline in passenger marine travel. In any event, there's no
doubt that many students can now keep readily and affordably at hand the technology
needed to perform a huge share of the algorithms usually encountered even in tertiary
mathematics. It's well known, for instance, that the TI-89 handles integrals, derivatives,
partial fractions , and much more. But did you know that the TI-89 can also
handle many of the residue calculations given as exercises in complex analysis texts?
With powerful computer algebra systems such as Maple and Mathematica also becoming
more affordable and available to students, the technology background has shifted
markedly.

With the desert island argument no longer operable, technology opponents resort to
other arguments. Technology takes too much time to learn, students can't think in the
presence of machines, technology use is just a post-modern cover for dumbing courses
down-another nail in the co n of civilization. I find these arguments unconvincing at
best and dishonest at worst. For instance, how much do you think your students really
struggle with technology as they pirate music MP3s from the Web? The dumbing-down
argument may be worst of all. it is simple "calumny" (as Tony Ralston put it in [2])
to equate technology-based reform with lowered intellectual standards or expectations.

This is not to deny, on the other hand, the existence of good, important, and (in
my opinion) still open questions surrounding pedagogical uses of technology. Owning a
calculator that "knows" how to expand rational functions in partial fractions does not
necessarily obviate the need to understand something of the idea-and perhaps even of
the process-by hand or by head.

At the school level, arguments over technology use often touch on the role and
importance of paper and pencil arithmetic (PPA) in technology-rich environments. At
one extreme are calculator abolitionists, asserting (with perhaps more vehemence than
evidence) that calculator use is somehow inimical to reason-children can be taught
to push buttons or to think, but not both. At the opposite end of the spectrum are
other abolitionist, such as Tony Ralston, who advocate abolition not of calculators but
of PPA as an explicit goal of K-12 mathematics education. (In his eloquent paper [2],
Ralston also recommends greatly increased emphasis on mental arithmetic, and perhaps
also on mental algebra.)

Coexisting with this clash of opinions is some basic agreement on ultimate goals.
In the end, most of us care far more about whether students can pose and solve novel
and challenging problems than about what technology might be used along the way.
What counts most is effective mathematical thinking, which comprises such elements as
basic symbol sense and facility with mathematical structures. What is mainly at issue,
I believe, is whether technology can help or must hurt the cause of teaching students
to think well mathematically.

Number sense and symbol sense

At the elementary level, what may really matter less than PPA facility and speed is
number sense, that intuition for numbers that includes such things as an ability to
estimate magnitudes, an eye for obviously wrong answers, and an instinct for choosing
(rather than necessarily performing) the arithmetic operation needed to solve a given
problem.

At the secondary and tertiary levels, the mathematical symbols under study become
much more general than numerals, and the degree of abstraction tends to rise as students
progress. The objects symbols stand for in more advanced mathematics might
be unknown numerical quantities, functions, operators, spaces of various sorts, or even
more abstract objects. At these higher levels of study the analogue of number sense is
"symbol sense," as defined by Arcavi[1] and others. Symbol sense is harder to define
and delimit than number sense-appropriately enough, given the greater mathematical
depth and breadth of, say, polynomial algebra as compared to integer arithmetic.
(Arcavi lists at least seven aspects of symbol sense-only one of which involves actual
symbolic manipulation.) Arcavi links symbol sense closely to algebra in particular-
acquisition of symbol sense is the proper goal of teaching algebra. For example, a
student with good symbol sense should sense that something is amiss with an "equation"
like

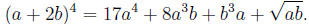
She should also know-without calculation-that of

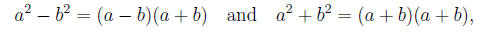
one is right and one is wrong, and that equations of the form

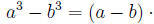something and 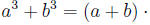something
can be arranged to hold, while

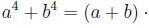something

is unpromising.
In this paper I want to take very broad views of both "symbol sense" and "algebra."
By symbol sense I mean a very general ability to extract mathematical meaning and
structure from symbols, to encode meaning effciently in symbols, and to manipulate
symbols effectively to discover new mathematical meaning and structure. By "algebra"
I mean symbolic operations in general, including not only algebra in the classical sense
but also such things as formal differentiation and expansion in power series.

Definitions may differ, but whatever one means exactly by "symbol sense", it's clear
that tertiary-level mathematics takes a lot of it. Tertiary mathematics is a symbolrich
domain, and doing mathematics successfully at this level requires considerable
comfort and sophistication with symbols. Above all, students need a clear sense of the
things symbols represent, and how to extract meaning and structural information from
symbolic expressions.

Perhaps this should all go without saying-who could doubt that symbols ought
to mean something to students? In practice, however, we've all seen students floating
freely in the symbolic ether, blithely manipulating symbols but seldom touching any
concrete mathematical ground. For example, many students struggle to make sense of
a symbolic expression such as

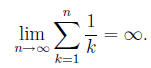
This is hardly surprising, after all, the statement's truth or falsity is far from obvious
to a newcomer to infinite series. But a more basic source of difficulty, I believe, is that
the expression's meaning-let alone its truth or falsity-is highly compressed in the
symbolic representation. "Unpacking" the symbolism to reveal meaning and structure
can be a daunting challenge in its own right, as we see when students confuse or con ate
the terms and the partial sums of an infinite series.
This brings me to my main questions.

1. How can we use technology-and symbol-manipulating technology in particular-
to help students acquire symbol sense in the broad sense discussed above?
2. Where does better symbol sense lead? How can students use better symbol sense
to understand mathematics more profoundly?