Cholesky Factorization

Abstract

This article, aimed at a general audience of computational scientists,
surveys the Cholesky factorization for symmetric positive definite
matrices, covering algorithms for computing it, the numerical
stability of the algorithms, and updating and downdating of the factorization.
Cholesky factorization with pivoting for semidefinite matrices
is also treated.

Keywords: Cholesky factorization, Cholesky decomposition, symmetric matrix,
positive definite matrix, positive semidefinite matrix, complete pivoting, partitioned
algorithm, level 3 BLAS, downdating, updating, stability, rounding error
analysis

AMS subject classifications. 65F05, 15A23

Introduction

A symmetric n×n matrix A is positive definite if the quadratic form x^TAx is
positive for all nonzero vectors x or, equivalently, if all the eigenvalues of A are
positive. Positive definite matrices have many important properties , not least
that they can be expressed in the form A = X^TX for a nonsingular matrix X.
The Cholesky factorization is a particular form of this factorization in which
X is upper triangular with positive diagonal elements; it is usually written
A = R^TR or A = LL^T and it is unique. In the case of a scalar (n = 1), the
Cholesky factor R is just the positive square root of A. However, R should in
general not be confused with the square roots of A, which are the matrices Y
such that A = Y ², among which there is a unique symmetric positive definite
square root, denoted A^1/2 [9, Sec. 1.7].

The Cholesky factorization (sometimes called the Cholesky decomposition)
is named after Andr´e-Louis Cholesky (1875–1918), a French military
officer involved in geodesy [3]. It is commonly used to solve the normal
equations A ^TAx = A^T b that characterize the least squares solution to the
overdetermined linear system Ax = b.

A variant of Cholesky factorization is the factorization A = LDL^T , where
L is unit lower triangular (that is, has unit diagonal) and D is diagonal. This
factorization exists and is unique for definite matrices. If D is allowed to
have nonpositive diagonal entries the factorization exists for some (but not
all) indefinite matrices. When A is positive definite the Cholesky factor is
given by R = D^1/2L^T .

Computation

The Cholesky factorization can be computed by a form of Gaussian elimination
that takes advantage of the symmetry and definiteness. Equating (i, j)
elements in the equation A = R^TR gives

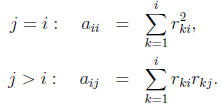
These equations can be solved to yield R a column at a time, according to
the following algorithm:

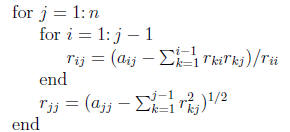
The positive definiteness of A guarantees that the argument of the square
root in this algorithm is always positive and hence that R has a real , positive
diagonal. The algorithm requires n³/3+O(n²) flops and n square roots, where
a flop is any of the four elementary scalar arithmetic operations +,−, ∗, /.

The algorithm above is just one of many ways of arranging Cholesky
factorization, and can be identified as the “jik” form based on the ordering of
the indices of the three nested loops. There are five other orderings, yielding
algorithms that are mathematically equivalent but that have quite different
efficiency for large dimensions depending on the computing environment,
by which we mean both the programming language and the hardware. In
modern libraries such as LAPACK [1] the factorization is implemented in
partitioned form, which introduces another level of looping in order to extract
the best performance from the memory hierarchies of modern computers. To
illustrate, we describe a partitioned Cholesky factorization algorithm. For a
given block size r, write

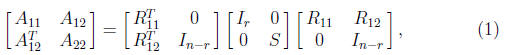
where A₁₁ and R₁₁ are r×r. One step of the algorithm consists of computing
the Cholesky factorization 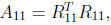solving the multiple right -hand side
triangular system 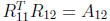for R₁₂, and then forming the Schur complement
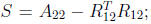; this procedure is repeated on S. This partitioned
algorithm does precisely the same arithmetic operations as any other variant
of Cholesky factorization, but it does the operations in an order that permits
them to be expressed as matrix operations. The block operations defining
R12 and S are level 3 BLAS operations [4], for which efficient computational
kernels are available on most machines. In contrast, a block LDL^T factorization
(the most useful form of block factorization for a symmetric positive
definite matrix) has the form A = LDL^T , where

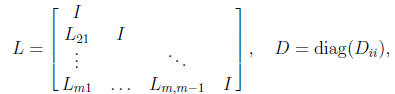
where the diagonal blocks D_ii are, in general, full matrices. This factorization
is mathematically different from a Cholesky or LDL^T factorization (in fact,
for an indefinite matrix it may exist when the factorization with 1×1 blocks
does not). It is of most interest when A is block tridiagonal [8, Chap. 13].

Once a Cholesky factorization of A is available it is straightforward to
solve a linear system Ax = b. The system is R^TRx = b, which can be solved
in two steps , costing 2n² flops:

1. Solve the lower triangular system R^T y = b,

2. Solve the upper triangular system Rx = y.

Numerical Stability

Rounding error analysis shows that Cholesky factorization has excellent numerical
stability properties. We will state two results in terms of the vector
2-norm 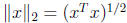and corresponding subordinate matrix norm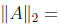
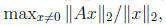where for symmetric A we have :
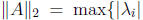λ_i is an eigenvalue of A}. If the factorization runs to completion in floating
point arithmetic, with the argument of the square root always positive, then
the computed 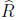satisfies

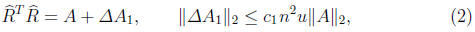
where a subscripted c denotes a constant of order 1 and u is the unit roundoff
(or machine precision). Most modern computing environments use IEEE
double precision arithmetic, for which u = 2^-53 ≈ 1.1×10^-16. Moreover, the
computed solution 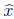to Ax = b satisfies

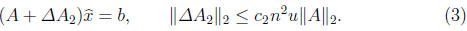
This is a backward error result that can be interpreted as saying that the
computed solution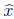 is the true solution to a slightly perturbed problem.
The factorization is guaranteed to run to completion if
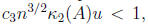
where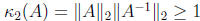is the matrix condition number with respect
to inversion. By applying standard perturbation theory for linear systems to
(3) a bound is obtained for the forward error:

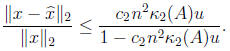
The excellent numerical stability of Cholesky factorization is essentially
due to the equality 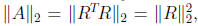which guarantees that R is of
bounded norm relative to A. For proofs of these results and more refined
error bounds see [8, Chap. 10].

Semidefinite Matrices

A symmetric matrix A is positive semidefinite if the quadratic form x^TAx is
nonnegative for all x; thus A may be singular. For such matrices a Cholesky
factorization A = R^TR exists, now with R possibly having some zero elements
on the diagonal, but the diagonal of R may not display the rank of A. For
example,

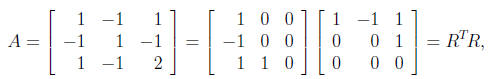
and A has rank 2 but R has only one nonzero diagonal element. However,
with P the permutation matrix comprising the identity matrix with its
columns in reverse order, 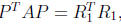, where

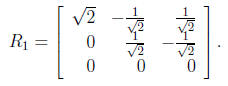
More generally, any symmetric positive semidefinite A has a factorization

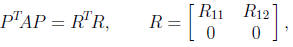
where P is a permutation matrix, R₁₁ is r×r upper triangular with positive
diagonal elements, and rank(A) = r. This factorization is produced by using
complete pivoting, which at each stage permutes the largest diagonal element
in the active submatrix into the pivot position. The following algorithm
implements Cholesky factorization with complete pivoting and overwrites
the upper triangle of A with R. It is a “kji” form of the algorithm.

Set p_i = 1, i = 1: n.
for k = 1: n
Find s such that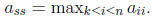
Swap rows and columns k and s of A and swap p_k and p_s.

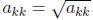
for j = k + 1: n
a_kj= a_kj/a_kk
end

for j = k + 1: n
for i = k + 1: j
a_ij= a_ij − a_kia_kj
end
end
end
Set P to the matrix whose jth column is the p_jth column of I.
An efficient implementation of this algorithm that uses level 3 BLAS [6] is
available in LAPACK Version 3.2. Complete pivoting produces a matrix R
that satisfies the inequalities

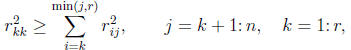
which imply r₁₁ ≥ r₂₂ ≥ · · · ≥ r_nn.
An important use of Cholesky factorization is for testing whether a symmetric
matrix is positive definite. The test is simply to run the Cholesky
factorization algorithm and declare the matrix positive definite if the algorithm
completes without encountering any negative or zero pivots and not
positive definite otherwise. This test is much faster than computing all the
eigenvalues of A and it can be shown to be numerically stable: the answer is
correct for a matrix A+ ΔA with ΔA satisfying (2) [7]. When an attempted
Cholesky factorization breaks down with a nonpositive pivot it is sometimes
useful to compute a vector p such that p^TAp ≤ 0. In optimization, when
A is the Hessian of an underlying function to be minimized, p is termed a
direction of negative curvature. Such a p is the first column of the matrix

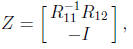
where [R₁₁ R₂₂ ] is the partially computed Cholesky factor, and this choice
makes p^TAp equal to the next pivot, which is nonpositive by assumption.
This choice of p is not necessarily the best that can be obtained from Cholesky
factorization, either in terms of producing a small value of p^TAp or in terms
of the effects of rounding errors on the computation of p. Indeed this is a
situation where Cholesky factorization with complete pivoting can profitably
be used. For more details see [5].

Updating and Downdating

In some applications it is necessary to modify a Cholesky factorization A =
RTR after a rank 1 change to the matrix A. Specifically, given a vector x
such that A − xx^T is positive definite we may need to compute 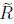such that
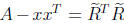(the downdating problem), or given a vector y we may need
to compute 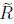such that 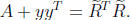For the updating problem write


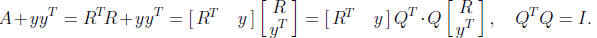
We aim to use the orthogonal matrix Q to restore triangularity; thus, for
n = 3, for example, we want Q to effect, pictorially,

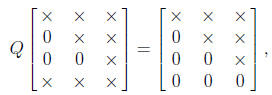
where × denotes a nonzero element. This can be achieved by taking Q as
a product of suitably chosen Givens rotations. The downdating problem
is more delicate because of possible cancellation in removing xx^T from A,
and several methods are available, all more complicated than the updating
procedure outlined above. For more on updating and downdating see [2,
Sec. 3.3].