1 Introduction
As our statistical models become more complicated, expressing them in matrix
algebra (also
known as linear algebra ) becomes more important. This lets us present our models
in a simple and
uncluttered format. All of the estimation of our statistical models, from OLS
through the most
complicated models we will study, is based on matrices. It will be in our best
interests to have a
clear understanding of how matrix algebra works .
A matrix is a rectangular array of numbers. We usually use bold-face
letters to indicate a
matrix. For example:
Each element in the matrix is subscripted to denote its
place. The row is the first number, and
the column is the second number. That is, elements in a matrix are listed as
.
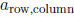A vector is an ordered set of numbers arranged in either a row or a column. A
row vector has
one row:
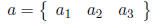
while a column vector has one column:
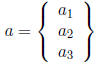
We usually denote a vector with a bold-face lower-case
letter.
A matrix can also be viewed as a set of column vectors or row vectors. The
dimension of a
matrix is the number of rows and columns it contains. We say “A is a n × k
matrix, where n is
the number of rows and k is the number of columns.
• If n = k, A is a square matrix .
• If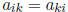 
, then A is a
symmetric matrix. For example:
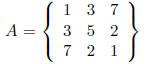
• A diagonal matrix is a square matrix whose only
non-zero elements are on the main diagonal
(from upper left to lower right ):
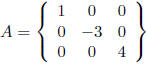
• A triangular matrix is a square matrix that has
only zeros either above or below the main
diagonal. If the zeros are above the diagonal, the matrix is lower triangular :
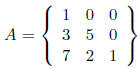
If the zeros are below the diagonal, the matrix is
upper triangular:
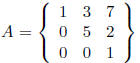
• An identity matrix is all zeros off the main
diagonal, and ones down the main diagonal. It
is usually denoted as I. For example, a 3 × 3 identity matrix is:
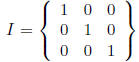
Here are several matrix operations and relationships you
should know.
• Equality of matrices. Two matrices A and B are equal if and only if they have
the same
dimensions and each element of A equals the corresponding element of B. That is,
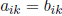
for all i and k.
• Transposition. The transpose of a matrix A is denoted A’, and is
obtained by creating the
matrix whose kth row is the kth column of the original matrix. Thus, if
A is n ×
k, A’ will
be k × n. For example:
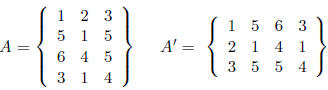
Note the transpose of a row vector is a column vector, and
vice-versa.
• Matrix addition. Matrices cannot be added together
unless they have the same dimension, in
which case they are said to be conformable for addition. To add two matrices we
simply
add the corresponding elements in each matrix. That is, A+B =
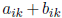for all i
and k. Of
course, addition is commutative (A+B = B +A), and subtraction works in the same
way as
addition. Matrix addition is also associative, meaning (A + B) + C = A + (B +
C).
• Matrix multiplication. Matrices are multiplied by using the inner product
(also known as
the dot product). The inner product of two vectors is a scalar (a constant
number). We
take the dot product by multiplying each element in the row matrix by the
corresponding
element in the column matrix. For example:
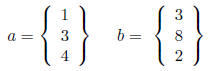
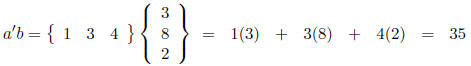
Note that a'b = b'a.
In order to multiply two matrices, the number of columns in the first must be
equal to the
number of rows in the second. If this is true the matrices are said to be
conformable for
multiplication. If we multiply a n × T matrix with a T × k matrix, the result is
a n × k
matrix. For example
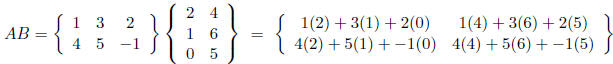
Multiplication of matrices is generally not commutative
(AB ≠ BA generally). Multiplying
a matrix by a scalar just multiplies every element in the matrix by that scalar.
That is,
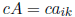for all i and k.
• Inverse Matrices. The inverse of a matrix A is denoted A-1. A-1 is constructed
such that
A-1A = I = AA-1. These are often difficult to compute (but that’s what computers
are for).
