Basic Rules for Logarithms

DEFINITION OF NOTATION: log_b x = y is equivalent to b^y = x

In other words, log _b x = y means the same thing as b^y = x

NOTE: In the rules below it is assumed that b > 0, b ≠ 1, M > 0, N > 0, and p is any real number.

I. log _b1 = 0

II. log _bb = 1

III. log _bb^x = x

IV. 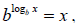where x > 0 .

V. log _b(M ٠ N) = log_bM + log_bN

VI.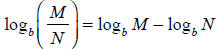

VII.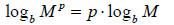 [NOTE: This rule is often used when solving exponential equations.]

VIII. If log _b x = log_b y, then x = y . This is true because f (x) = log_b x is a 1 - 1 function.

IX.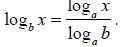 [NOTE: This is known as the Change of Base Formula.]

X. If log _b x = y , then b^y = x . This comes from the basic definition at the top of this page.

XI. If b^x = b^y , then x = y . This is true because f (x) = log_b x is a 1 - 1 function.
------------------------------------------------------------------------------------------------------------------------------

NOTE: Rules III and IV are true becausef (x) = log_b x and f (x) = b^x are inverses of each other.
Therefore,(g ◦ f )(x) = x and ( f ◦ g)(x) = x .

NOTE: Rules VIII and X are frequently used when solving log equations.

NOTE: Rule XI is sometimes used when solving exponental equations. It is easy to show that Rule XI
is true, because Rule III is true.